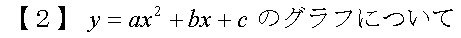
【1】の性質が理解できたら,一般形の2次関数のグラフへ進もう.



|
さらに,数学Ⅱの積分を若干使ってみよう.放物線には面積に関して非常に単純な性質がある.
|
《性質2―1》~放物線の等比分割性
|
(解 説)
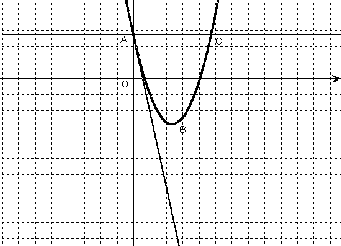
さらに,【1】の切片形のグラフに話を戻してみよう.
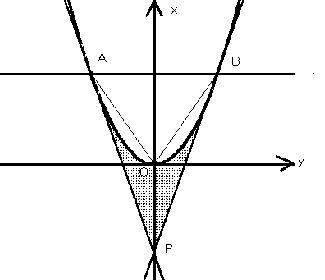
x軸との2交点O,Bにおける接線の交点Pと直線OBについては,それぞれ放物線の極,極線と呼ばれる.2接線と極線で囲まれた三角形の面積は,極線,頂点を通り極線に平行な直線 (ここではx軸),接点を通り軸に平行な2直線で囲まれる四角形の面積に等しくこれをSとする.(∵【1】の性質 4゜より PB=BM)
《性質2-2》2接線と放物線で囲まれる図形の面積は
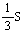 となる. となる.
|
《性質2-3》頂点と接点を結ぶ2直線と放物線によって囲まれた図形の面積は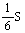 となる. となる.
|
|