丂戝愄丄恖娫偼乮侾乯偲偄偆悢偑昁梫偱偁偭偨丅偦傟偼丄帺暘偺曔偭偰偒偨嫑傗廱丄壠抺偺悢傪悢偊傞偨傔偱偁偭偨丅師戞偵丄暥壔偑敪払偡傞偵偮傟丄暔偺挿偝傗搚抧偺柺愊傪應傞傛偆偵側偭偰偒偨丅偡傞偲丄嘆乮侾乯偩偗偱偼昞偟偒傟側偄敿抂側検偑偱偰偔傞傛偆偵側偭偨丅偦偺敿抂側悢傪昞偡偨傔偵憂傜傟偨偺偑乮俀乯偱偁傞丅偙傟偵傛傝丄偦傟傑偱應傝偒傟側偐偭偨挿偝傗柺愊傑偱嵶偐偔悢帤偱昞偣傞傛偆偵側偭偨丅
丂暥柧偑偱偒偁偑偭偰丄恾宍偵娭偡傞尋媶偑懡偔側偝傟傞傛偆偵側偭偨丅僊儕僔傾偺僺僞僑儔僗妛攈傕偦偺尋媶側偳傪偟偰偄偨丅偲偙傠偑丄偁傞偲偒偵嘇嫵夛偺揤堜偺恾暱傪傒偰丄嘊桳柤側掕棟傪敪尒偟偨偺偩偑丄偦傟偵傛傝乮侾乯偱傕乮俀乯偱傕昞偣側偄曈偺挿偝傪敪尒偟偰偟傑偭偨丅偙傟偑乮俁乯偱偁傞丅摉帪偼乽偡傋偰乮侾乯傪巊偭偰悢傪昞偣傞乿偲摉慠偺傛偆偵峫偊偰偄偨偺偱丄乮侾乯帺懱偱傕丄傑偨丄偦傟傪巊偭偰昞偟偨乮俀乯偱傕昞偣側偄乮俁乯傪乽摴棟偵崌傢側偄悢乿偲偟偰峫偊偨丅
丂彜岺嬈偑敪払偟偰偔傞偲丄柉廜偵乮係乯偺奣擮偑傔偽偊偰偔傞偙偲偵側傞丅嘋嵿嶻偵懳偟偰偺乽庁嬥乿丄億乕僇乕偱偺摼揰偵懳偡傞乽幐揰乿偲偄偆斀懳偺奣擮傪昞偡傕偺偲偟偰堢偭偰偒偨丅偟偐偟丄幚嵺偵偼僀儞僪偱俀師曽掱幃偺夝偺尋媶偱僶僗僇儔乮12俠崰乯偵妋棫偝傟偰偄傞丅
丂16俠枛丄儀儖僊乕偺僗僥償傿儞偼丄嘍棙巕偺寁嶼偱傢偐傝傗偡偔丄娙扨偵埖偊傞悢偲偟偰憂偭偨偺偑乮俆乯偺巒傑傝偲偄傢傟偰偄傞丅
栤侾丂嬻棑侾偐傜俆偵摉偰偼傑傞悢傪娍帤偱彂偗丅
栤俀丂朤慄嘆偵偮偄偰丄崱偐傜係侽侽侽擭傎偳慜偺偙偲偑彂偐傟偰偄傞乽傾乕儊僗偺僷僺儖僗乿偵師偺傛偆側婰弎偑偁傞丅
丂丂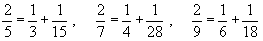
偙傟偼丄乽俀偮偺傕偺傪悢恖偱暘偗傞乿偲偒偺偨傔偵嶌傜傟偨幃偲峫偊傜傟傞偑丄嵟弶偵偁傞
丂丂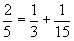
偲側傞棟孅傪恾側偳巊偭偰愢柧偣傛丅
乮溯膩F乽俀偮偺傕偺傪俆恖偱暘偗傞乿偙偲傪峫偊傞乯
栤俁丂朤慄嘇偵偮偄偰丄偳傫側恾暱傪傒偰敪尒偟偨偺偐丅偦偺恾暱傪奊偵昤偗乮朤慄嘊偺億僀儞僩偲側傞奊偱傛偄乯丅
栤係丂朤慄嘊偼壗偲偄偆掕棟偐丅師偺嬻棑偵娍帤嶰帤傪摉偰偼傔傞偙偲偱摎偊傛丅
丂丂乮丂丂丂丂丂丂丂丂乯偺掕棟
栤俆丂朤慄嘋偵偮偄偰丄乽嵿嶻乿偲乽庁嬥乿偺傛偆偵乽亄乿偲乽亅乿偺娭學偱昞偣傞傕偺偺椺傪堦偮嫇偘傛丅
丂丂乮夝摎椺丗乽嵿嶻乿偲乽庁嬥乿乯
栤俇丂朤慄嘍偵偮偄偰丄偳偪傜偺嬧峴偵梐偗傞曽偑摼偱偁傞偐丅
丂丂俲嬧峴丂擭棙丂110/664丂丂丂倂嬧峴丂擭棙丂1143/8884
丂乮椺乯乽侾侽侽恑朄乿仺乽100慘乿偼乽侾墌乿偵側傞
丂乮侾乯乽俇侽恑朄乿
丂乮俀乯乽侾俀恑朄乿
丂乮俁乯乽俀恑朄乿
|
侾丂丂僱僞僢僩 俀丂丂僱僀僗 俁丂丂僱僀僗亖僱僞僢僩 係丂丂僱僀僗亖僱僀僗 |
栤侾丂偙偺婯懃偐傜丄乽俈乿偼偳偺傛偆偵昞偝傟傞偲悇應偱偒傞偐丅
栤俀丂乽僱僀僗亖僱僀僗亖僱僀僗亖僱僀僗亖僱僀僗亖僱僀僗亖僱僞僢僩乿偼偄偔偮傪昞偡偲悇應偱偒傞偐丅
栤俁丂傢傟傢傟偼乽侾丆俀丆俁丒丒丒乿側偳偺傾儔價傾悢帤傪擔忢偱巊梡偟偰偄傞丅僩儗僗奀嫭偺搰乆偺恖偨偪偺悢帉偲傾儔價傾悢帤傪斾妑偟偰丄慜幰偺乽棙揰乿偲乽寚揰乿偵偮偄偰婰偣丅
丂亙棙揰亜
丂亙寚揰亜
| 嘥 | 侾 | 丂 | 俴 | 俆侽 | 丂 | 嘥乯 | 俆侽侽 |
| 嘦 | 俀 | 丂 | 倃俠 | 俋侽 | 丂 | 乮嘥乯 | 侾侽侽侽 |
| 嘨 | 俁 | 丂 | 俠 | 侾侽侽 | 丂 | 嘥乯乯 | 俆侽侽侽 |
| 嘩 | 係 | 丂 | 俢 | 俆侽侽 | 丂 | 乮乮嘥乯乯 | 侾侽侽侽侽 |
| 嘪 | 俆 | 丂 | 俠俵 | 俋侽侽 | 丂 | 嘥乯乯乯 | 俆侽侽侽侽 |
| 嘫 | 俇 | 丂 | 俵 | 侾侽侽侽 | 丂 | 乮乮乮嘥乯乯乯 | 侾侽侽侽侽侽侽 |
| 嘮 | 俈 | 丂 | 丂 | 乮乮乮乮嘥乯乯乯乯 | |||
| 嘯 | 俉 | 丂 | 丂 | ||||
| 嘰 | 俋 | 丂 | 丂 | ||||
| 嘳 | 侾侽 | 丂 | 丂 |
乮椺乯嘳俢俠嘳嘳嘩乮侾俇俀係乯
栤侾丂師偺悢傪儅儎偺悢昞婰偱昞偣丅
丂乮侾乯侾俀丂丂丂丂丂丂乮俀乯俁係俆
丂乮俁乯侾俀侽俉丂丂丂丂乮係乯侾俈俁俀侽
栤俀丂師偺寁嶼傪偣傛乮夝摎偼儅儎偺悢帉偱偣傛乯丅
乮侾乯俠俠倃倃倃倃倁嘨亄俠俴倃倃嘨
乮俀乯俵俵俵CM俴倃倃亅俬乯XC嘯
乮侾乯暯峴巐曈宍
乮俀乯戜宍
| 墌偺柺愊偼丄捈宎偐傜偦偺侾乛俋傪傂偄偨傕偺偺俀忔偵摍偟偄丅 |
偙傟偵偮偄偰師偺栤偵摎偊傛丅
栤侾丂捈宎傪俀倰丄柺愊傪俽偲偟偰偙傟傪棫幃偣傛丅
栤俀丂慜栤偺寢壥偐傜丄偙偺偙傠偺僄僕僾僩恖偱偼丄墌廃棪兾偼偄偔偮偲偲傜偊偰偄偨偙偲偵側傞偐乮彫悢戞俀埵傑偱傪夝摎偣傛乯丅
丂丂俽亖兾倎俀 偙偺偙偲偲僇僶儕僄儕偺尨棟傪巊偭偰懭墌偺柺愊傪媮傔傞偙偲偵偡傞丅懭墌偲偼師偺傛偆側恾宍偱偁傞丅
乮侾乯僇僶儕僄儕偺尨棟偐傜師偺斾傪媮傔傛丅
丂丂丂乮墌偺柺愊乯丗乮懭墌偺柺愊乯
乮俀乯慜栤偐傜懭墌偺柺愊傪媮傔傛丅