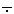�@���i�T�O�́j�l�Ԃ���������Ɠ����ɍ��ꂽ
�p�D�Ȃ��u���R���v�͕K�v�������̂��H
�`�D���������L���i�̎���ƒ{�Ȃǁj�̐����m���߂�����������B
�@�@�@�@�@��
��̂Ɂu�����v�̂Ȃ�������������
�@�@�@�@�@��
�u���m�v���g���ċL�^����
�@�i��j���E��̌��іځi���L���Ƃ́u�P�P�Ή��v�j
�@�@�@�@�@��
�u�����v�̒a��
�@�i��j�E�M���V�A�����i���C���C���E�E�E�j
�@�@�@�@�E���[�}�����@�i�T�C�U�C�V����j
�@�@�@�@�E�A���r�A�����i�P�C�Q�C�R����j
�@�@�@�@�E�������@�@�@�i��C��C�O����j
�@�@�@�@�@���u�����̑���v�������Ă���
�@�@�@���@���K�v�����g�Q��
�p�D�Ȃ��u�����v���K�v�ɂȂ����̂�
�`�D�u�Ђ��̒����̔�ׂ����v
|
�Q�Q�Q�Q�Q�Q�Q�Q�Q�Q�Q�Q�Q �Q�Q�Q�Q�Q�Q�Q�Q�Q |
�u��̂Ђ��͉��̂Ђ��ɔ�ׂĂǂꂾ�������̂��v
�u�����v�𑪂�i�h�P�ʁh������j
�@�@�@�@�@��
�u���[�v�Ȓ������]��
�@�@�@�@�@��
�u���[�v��\�����߂ɁA�u�����v���a�������I
�u�����v���u�L�䐔�v�G�i���R���́j��ŕ\����鐔
�@�@�@�@�@�u�L�����v�G�i���R���ŕ\����Ƃ����Ӗ��Łj�����ɂ��Ȃ�����
���̂̐l�����́u���̒��̂��ׂĂ̐��́A�����̔�i�����j�ŕ\����v���Ƃ𐢂̒��́u�����v�Ƃ��Ă����B
�@�@�@�@�iB.C.20���I���j�G�W�v�g�u�����h�E�p�s���X�v�̋L�^�������̋L�^
�@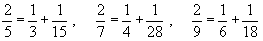 �@���@�ǂ����Ă���ȕ\����������̂��H
�@���@�ǂ����Ă���ȕ\����������̂��H
���P�̗\����
�Q���́g���m�h���T�l�ł킯��i�Q/�T�j
�@ �@���̂̐l�͒P�ʕ����i���q���P�j���g���Ă���
�@���̂̐l�͒P�ʕ����i���q���P�j���g���Ă���
�i�P�l������j�P/�R�~�P/�T���P/�P�T�@�@���@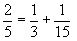
�E�u�s�^�S���X�iB.C.582-493���j�̒藝 �v�i�O�����̒藝�j
�i�����̕��@�j
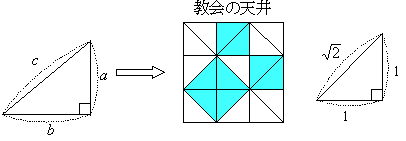
���Ƃ��u�L�����v�ŕ\�����Ƃ���
�@�@�@�@�@���h�\���Ȃ��h���h�����ɍ���Ȃ��h
�u�������v�̒a���I
| �@���̌�A�u�P�J�b�`���v�i�u�������v�Ƃ������O�̐��k�̃j�b�N�l�[���j�Ƃ��������̒P�ʂ�n���āA��Q�J�b�`�����R�J�b�`���ȂǁA�������ŕ\����钷���̍�}���o�肵���B |
�u�i�����j�� �i�Ԏ��j�v�̊W
�E�j����i�m�ʂ̂��������j
�@9,600,000�i�a���j�|700,000�i���Ẫ����N���j��8,900,000�i���Y�j
�@�@���@�u�������]���Ă���v�����Y�́u�����v
�E�v����i�D�y�̎؋����j
�@ �O�i�a���j�@�@�@�|3,200,000�i�V�Ԃ̃X�J�f�j���|2,500,000�i���Y�j
�@�@ ���@�u����������Ȃ��v�@�����Y�́u�Ԏ��v
���̏ꍇ�A�u�|�v�̕����́A�u�����v�Ƃ����̐����������Ă���
�@�@�@�@�@�u�O�v�̕����́A�u�����v�Ɓu�Ԏ��v�̋��ڂ������Ă���B
�͂�����Ɓu���v�̊T�O���ł����̂́A�P�Q�b��
�E�C���h�̐��w�҂̊���
�i��j�Q���������̉�@
�p�D�ʐς��W�P�̐����`������܂��B�P�ӂ̒����́H
�`�D�P�ӂ̒������ԂƂ����
�@�@���Q���W�P�@�@���@�ԁ��X
�@�����ƂȂ���̂́A�u���v�ɂȂ���̂������݂��Ȃ�����
�@�@�@�@�@ ��
�@�o�X�J���i12�b���j���Q���������̉��̌������������I
�@�u�Q���������ɂ́A�K���Q�̉������݂���v�G�u���v�̐��̔F��
�X�e���B���i�x���M�[�j�F��v���Z�i��v�E���q�̌v�Z�j
�E���q�̌v�Z
�@�u�����v�ɂ��v�Z
�@���ɂ���Ắu�����Â炢�v���u�����ɂ����v
�@�@�@�@�@��
�@�u10�O����Ƃ��������v�ɂ��v�Z
�@���������̂��r����Ƃ��A���ꂪ�P�O�O���œ��ꂳ��Ă���̂ŁA�O���͔�ׂ₷��
��241/1000��32641/100000�̑召�H
�@���p�b�ƌ��������ł͋�ʂł��Ȃ�
�@�@�@�@�@ �������̒a��
�i��j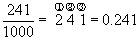
�@�@�@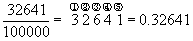 �@�@�˖�30�N��i�p�E�Ɓj
�@�@�˖�30�N��i�p�E�Ɓj
�@�@�@�@�@�@�@�@�@�i�X�e���B���j