 丂丂偙偺柺愊傪乽cm俀乿偲掕媊偟丄偙傟傪婎弨偲偡傞丅
丂丂偙偺柺愊傪乽cm俀乿偲掕媊偟丄偙傟傪婎弨偲偡傞丅
嘆婎杮乮扨埵乯
 丂丂偙偺柺愊傪乽cm俀乿偲掕媊偟丄偙傟傪婎弨偲偡傞丅
丂丂偙偺柺愊傪乽cm俀乿偲掕媊偟丄偙傟傪婎弨偲偡傞丅
嘇慄暘偱埻傑傟傞恾宍
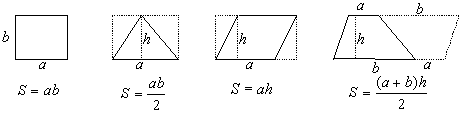
丒屆戙僄僕僾僩偺搚抧偺應検弍
丂僫僀儖愳偱掕婜揑側斆棓
丂仺敤偺嬫夋偺堷偒捈偟傪侾擭偵侾搙偟側偗傟偽側傜側偐偭偨亖應検弍偺敪払
嘊嬋慄偱埻傑傟偨恾宍嘥亅墌偺柺愊亅
丒僄僕僾僩
乽擆偼偦偺乮捈宎偺偙偲乯侾乛俋偱偁傞俀傪堷偔偙偲偵側傞丅巆傝偼侾俇偱偁傞丅擆偼侾俇傪侾俇攞偡傞寁嶼傪偡傞偙偲偵側傞丅偦傟偼俀俆俇偵側傞丅乿
俻丏偙偺暥復傪棫幃偣傛丅
俙丏乮侾俉亅侾俉仏侾乛俋乯丱俀亖俀俆俇
偙傟傪捈宎俀倰偲偟偰寁嶼偡傞偲丄
丂乮俀倰亅俀倰乛俋乯丱俀亖俽
丂丂亪俽亖俀俆俇乛俉侾仏倰丱俀
丂丂亪兾亖俀俆俇乛俉侾乮佮俁丏侾俇乯偲峫偊偰偄偨偙偲偵側傞
丂丂俽亖乮撪愙惓曽宍乯亄乮擇摍曈嶰妏宍乯仏係
丂丂仺寗娫傪偝傜偵擇摍曈嶰妏宍偱曗娫偟偰偄偗偽丄墌偺柺愊偵嬤偯偔
丂丂乽墌亖嶰妏宍偺愊傒廳偹乿仺嵶暘壔偡傞傎偳丄墌偺柺愊偵嬤偯偔
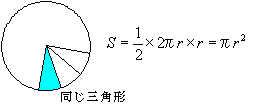
仸俽亖兾倰俀傪捈娤揑偵帵偡曽朄
嘆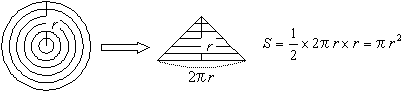
嘇
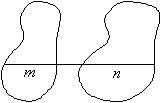 嘋嬋慄偱埻傑傟偨恾宍嘦亅嬫暘媮愊朄亅
嘋嬋慄偱埻傑傟偨恾宍嘦亅嬫暘媮愊朄亅
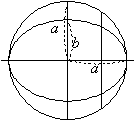 俻丏懭墌偼丄塃偺恾偺傛偆偵墌偺捈宎傪幉偲偟偰堦掕曽岦偵埑弅偟偨傕偺偲峫偊傜傟傞丅偙傟偲僇僶儕僄儕偺尨棟傪梡偄偰丄懭墌偺柺愊傪媮傔傛丅
俻丏懭墌偼丄塃偺恾偺傛偆偵墌偺捈宎傪幉偲偟偰堦掕曽岦偵埑弅偟偨傕偺偲峫偊傜傟傞丅偙傟偲僇僶儕僄儕偺尨棟傪梡偄偰丄懭墌偺柺愊傪媮傔傛丅
俙丏墌偺柺愊偼俽亖乮侾乯偱僇僶儕僄儕偺尨棟傛傝墌偲懭墌偺柺愊斾偼
丂丂乮侾乯丗乮懭墌乯亖乮俀乯丗乮俁乯
丂廬偭偰丄乮懭墌乯亖乮係乯
丒愊暘偵傛傞柺愊偺媮傔曽
丂僇僶儕僄儕偼丄捈慄偱柺愊偺斾傪昞偡偲偄偆曽朄偱丄乽柺愊乮俀師尦乯傪乽慄暘偺榓乮侾師尦乯乿偲偟偰帵偟偨丅偙偺峫偊曽傪敪揥偝偣偰偄偭偨偺偑僼僃儖儅乕乮暓乯偨偪偺峫偊偱偁傞丅
媮傔傞椞堟傪敄偔僗儔僀僗偟偰丆暆偑倓倶丆廲偑倖(倶)偺旝彫柺愊倖(倶)丒倓倶偺朹忬挿曽宍偵暘妱偡傞丅偙傟傜傪婑偣廤傔偨傕偺偑丆媮傔傞柺愊偱偁傞丅
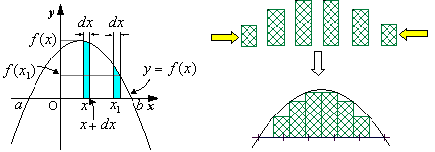
丂偙偺僼僃儖儅乕偨偪偺峫偊曽偲旝暘偺婎慴傪嶌傝忋偘偨偺偑僯儏乕僩儞乮塸乯偲儔僀僾僯僢僣乮撈乯偱偁傞丅偦偟偰丄尰嵼偺傛偆側昞偟曽傪偡傞傛偆偵側偭偨偺偑丄儕乕儅儞偵傛傞偺偱偙偺愊暘傪乽儕乕儅儞愊暘乿偲偄偆丅
俻丏暿巻偺恾偺柺愊傪丄僼僃儖儅乕偨偪偺峫偊曽傪巊偭偰挿曽宍偺榓偱嬤帡偡傞偙偲偵傛傝媮傔傛丅