〇複素数の認知について
「数学B」の複素数の単元の高次方程式の解法を終了した段階で,複素数の誕生の歴史について触れる。複素数が発見され、その概念が確立するまでの過程に触れることにより,生徒は新たな視点で複素数を理解することができる。
| 授業の流れ | 補 足 ・ 説 明 |
|---|---|
| カルダノについて |
・カルダノ(イタリア:1501-1576) ・著書 『アルス・マグナ(大技法),1545年』 (3次方程式の解の公式について) 「フェロが30年前に発見し、弟子のフィオーレ(フロリド)に教え,フィオーレがタルタリア(フォンタナ)と3次方程 式をめぐる数学試合をした際(1535年)に,タルタリアは自身で発見し,その後,私の切望に応じて,それを証明を添えな いで教えてくれた。」 |
| カルダノの公式 |
・x3=px+q(p>0,q>0)の解は,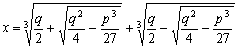 |
|
3次方程式 x3=15x+4を解く ① 因数定理を用いて ② カルダノの公式を用いて |
・解 x=4,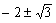 ・(2+i)3=2+11i,(2-i)3=2-11i 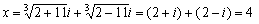
|
|
複素数の認知 カルダノの公式を用いて解くと,解法の途中に複素数が現れるのに,解そのものが実数になる。 |
・カルダノは大変驚き,このことをどう意味付けてよいか当惑したという。3次方程式では,複素数の存在を認めない限り, 実数の解さえ計算できないという矛盾に直面したのである。 |
連立方程式の解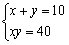 |
・当時の代数方程式では解としては正の実数解のみを考えていた。 ・カルダノは「10をその積が40になる2つの数へ分解することは不可能である」としながら,形式的な解として, 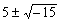 を示した。 を示した。
|