 偵偮偄偰丄巹傕摨偠傛偆側巊偄曽傪偟偰偄傑偡丅偙傫側尒曽偼偳偆偱偟傚偆偐丅
偵偮偄偰丄巹傕摨偠傛偆側巊偄曽傪偟偰偄傑偡丅偙傫側尒曽偼偳偆偱偟傚偆偐丅
丂悢妛偺偄偢傒俫俹偺幚慔婰榐丒儗億乕僩偵嵹偭偰偄傞丄嶥杫搶崅峑丂嵅摗丂惔愭惗偺儗億乕僩乽俀偮偺慄暘偺岎揰偺埵抲儀僋僩儖傗撪暘斾傪媮傔傞棤媄乮嫵巘梡乯乿傪撉傫偱丄宍偼偪偑偆幃偱偡偑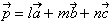 偵偮偄偰丄巹傕摨偠傛偆側巊偄曽傪偟偰偄傑偡丅偙傫側尒曽偼偳偆偱偟傚偆偐丅
偵偮偄偰丄巹傕摨偠傛偆側巊偄曽傪偟偰偄傑偡丅偙傫側尒曽偼偳偆偱偟傚偆偐丅
丂侾捈慄忋偵側偄俁揰俙丆俛丆俠偺埵抲儀僋僩儖傪偦傟偧傟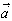 丆 丆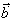 丆 丆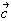 偲偡傞偲偒丄師偺偙偲傪徹柧偣傛丅 偲偡傞偲偒丄師偺偙偲傪徹柧偣傛丅(1)丂揰俹偑丄俙丆俛丆俠偺掕傔傞暯柺忋偵偁傞偨傔偵昁梫廫暘側忦審偼丄俹偺埵抲儀僋僩儖 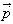 偑師偺宍偵彂偐傟傞偙偲偱偁傞丅 偑師偺宍偵彂偐傟傞偙偲偱偁傞丅丂丂丂 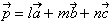 丆倢亄倣亄値亖侾 丆倢亄倣亄値亖侾(2)丂忋偺幃偱倢丆倣丆値偑偡傋偰惓側傜偽丄俹偼仮俙俛俠偺撪晹偵偁傞丅 |
乮徹柧乯
 (1)丂俹傪暯柺俙俛俠忋偺揰偲偡傞偲
(1)丂俹傪暯柺俙俛俠忋偺揰偲偡傞偲
丂丂丂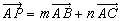 丂丒丒丒丒丒丂嘆
丂丒丒丒丒丒丂嘆
偲彂偗傞丅偙傟傪埵抲儀僋僩儖偱昞偡偲
丂丂丂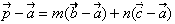 丂丒丒丒丒丒丂嘇
丂丒丒丒丒丒丂嘇
丂丂丂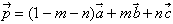 丂丒丒丒丒丒丂嘊
丂丒丒丒丒丒丂嘊
傛偭偰丄倢亖侾亅倣亅値偲偍偔偲
丂丂丂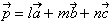 丆倢亄倣亄値亖侾丂丒丒丒丒丒嘋
丆倢亄倣亄値亖侾丂丒丒丒丒丒嘋
丂媡偵丄嘋偑惉傝棫偰偽丄嘊丆嘇丆嘆偑摫偐傟傞偐傜丄俹偼暯柺俙俛俠忋偵偁傞丅
(2)倢亜侽 丆倣亜侽丆値亜侽偺偲偒丄
丂丂丂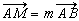
偲偍偔偲丄侽亙倣亙侾偩偐傜丄俵偼曈俙俛忋乮抂偼彍偔乯偺揰偲側傞丅偦偟偰丄嘆偐傜
丂丂丂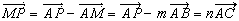 丂丒丒丒丒丒丂嘍
丂丒丒丒丒丒丂嘍
傛偭偰丄捈慄俵俹偼俙俠偲暯峴偱偁傞丅偙傟偲曈俛俠偲偺岎揰傪俻偲偡傞偲
俵俻丗俙俠亖俵俛丗俙俛亖乮侾亅倣乯丗侾偐傜
丂丂丂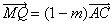 丂丒丒丒丒丒丂嘐
丂丒丒丒丒丒丂嘐
嘍丆嘐偱丄侾亅倣亖倢亄値亜値亜侽 偩偐傜丄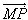 丆
丆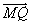 偼摨曽岦偱丄俵俹亙俵俻
偼摨曽岦偱丄俵俹亙俵俻
偟偨偑偭偰丄俹偼慄暘俵俻忋乮抂偼彍偔乯偵偁傞偐傜丄仮俙俛俠偺撪晹偵偁傞丅
丂偙偺偲偒丄拲栚偟偨偄偺偑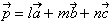 偲 仮俙俛俠 偺曈側偳偺撪暘斾偺娭學偱偡丅恾偺傛偆偵側偭偰偄偰丄(鶣),(鶤),(鶥)偺摿挜偑偁傝傑偡丅
偲 仮俙俛俠 偺曈側偳偺撪暘斾偺娭學偱偡丅恾偺傛偆偵側偭偰偄偰丄(鶣),(鶤),(鶥)偺摿挜偑偁傝傑偡丅
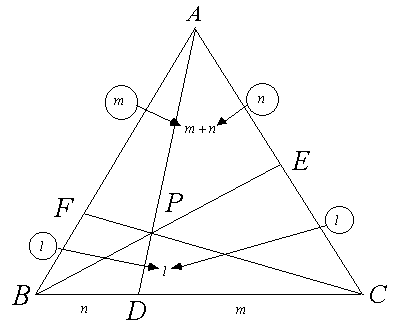
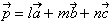 偺
偺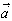 丆
丆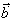 丆
丆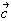 偺學悢偼丄捀揰俙(
偺學悢偼丄捀揰俙(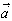 )偵懳偡傞曈俛俠偵娭偡傞斾偵弌偰偙側偄暥帤倢丆
)偵懳偡傞曈俛俠偵娭偡傞斾偵弌偰偙側偄暥帤倢丆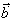 丆
丆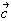 傕摨條偵倣丆値傪懳墳偡傞丅
傕摨條偵倣丆値傪懳墳偡傞丅
丂(鶣),(鶤),(鶥)傪巊偭偰丄嵅摗愭惗偺乵栤戣乶傪峫偊偰傒傑偡丅
乵栤戣乶
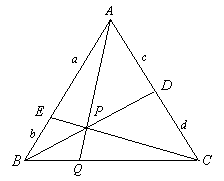 丂嶰妏宍俙俛俠偵偍偄偰丄
丂嶰妏宍俙俛俠偵偍偄偰丄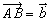 丆
丆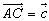 偲偟丄曈俙俛丆俙俠偺撪暘揰俢丆俤傪師偺傛偆偵掕傔傞丅
偲偟丄曈俙俛丆俙俠偺撪暘揰俢丆俤傪師偺傛偆偵掕傔傞丅
丂丂丂俙俢丗俢俛亖倎丗倐丆丂俙俤丗俤俠亖們丗倓
丂偙偺偲偒丄俢俠偲俛俤偺岎揰傪俹丄俙俹偲俛俠偺岎揰傪俻偲偡傞丅
(1) 俛俻丗俻俠偺斾傪媮傔傛丅
(2) 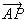 傪
傪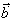 偲
偲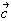 偱昞偣丅
偱昞偣丅
乵嶌恾乶
丂(鶣)傛傝俛俢偲俠俤偼摨偠抣偱懳墳偝偣傟偽傛偄偺偱丄倐偲倓偺嵟彫岞攞悢倐倓偵抲偒偐偊傑偡丅偙偺偲偒丄俙俢丆俙俤偼倎倓丆倐們偑懳墳偟(恾侾)丄倐倓丆倎倓丆倐們傪孞傝曉偡偺偱丄俛俻丆俻俠偵倐們丆倎倓傪懳墳偝偣傞(恾俀)丅偙偺偲偒丄俙俹丆俹俻偼(鶤)傛傝丄倎倓亄倐們丆倐倓偑懳墳丅
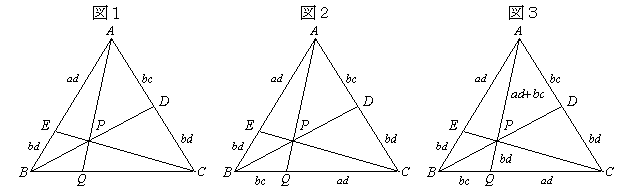
(1)丂恾俀傛傝丂俛俻丗俻俠亖倐們丗倎倓
(2)丂恾俁傛傝寁嶼偟偰傕椙偄偑丄(鶥)傪巊偆偲
丂丂丂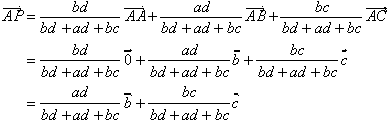
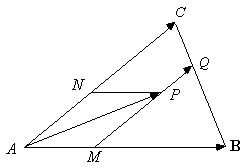
栤戣侾丂仮俙俛俠偵偍偄偰慄暘俙俛傪俀丗侾偵撪暘偡傞揰傪俵偲偟丄慄暘俙俠傪俁丗俀偵撪暘偡傞揰傪俶偲偡傞丅傑偨丄俀偮偺慄暘俠俵偲俛俶偲偺岎揰傪俹偲偟丄捈慄俙俹偲曈俛俠偲偺岎揰傪俻偲偡傞丅偙偺偲偒
(1)儀僋僩儖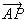 傪
傪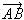 丄
丄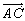 偱昞偣丅
偱昞偣丅
(2)儀僋僩儖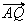 傪
傪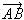 丄
丄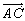 偱昞偣丅
偱昞偣丅
(3)柺愊偺斾 仮俙俛俹丗仮俛俠俹丗仮俠俙俹 傪媮傔傛丅
栤戣俀丂暯柺忋偵仮俙俛俠偲揰俹偑偁傝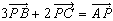 偱偁傞丅偙偺偲偒仮俹俙俛丄仮俹俛俠丄仮俹俠俙 偺柺愊斾傪媮傔傛丅
偱偁傞丅偙偺偲偒仮俹俙俛丄仮俹俛俠丄仮俹俠俙 偺柺愊斾傪媮傔傛丅