|
漸近展開に関するメモ
Landau の記号と漸近展開
ver1.3
京都府立鳥羽高校定時制 稲葉芳成
はじめに
この文章は, 大学初年度向けの微分積分のテキストである, 「三宅敏恒著『入門微分積分』培風館」を参考にして, 内容が平易でしかも有用である漸近展開について再構成してまとめたメモです.
漸近線
双曲線
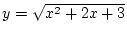 の漸近線を考えるには の漸近線を考えるには 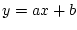 に対して に対して
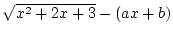 を考えれば を考えれば
によって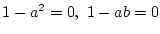 より より 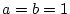 を得ます. を得ます.
一方
という具合に展開できることから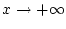 で で 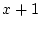 に近づく感じがわかると思います. その様子を見ると
となりますが漸近線という考えから, 右辺を左辺の に近づく感じがわかると思います. その様子を見ると
となりますが漸近線という考えから, 右辺を左辺の 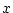 が大きいところでの評価式と考えれば が大きいところでの評価式と考えれば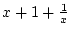 に近づく感じもまたわかります.
さてここで展開式にもどって眺めると に近づく感じもまたわかります.
さてここで展開式にもどって眺めると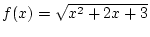 は は
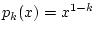 と置くときに
の形に展開されていると見れます. と置くときに
の形に展開されていると見れます.
この式は項が後になるほど 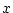 の大きいところでは小さい値をとることから, 展開を有限項でうち切ったときに, 剰余項は十分小さいものとなることが感覚的にわかるでしょう. そこで の大きいところでは小さい値をとることから, 展開を有限項でうち切ったときに, 剰余項は十分小さいものとなることが感覚的にわかるでしょう. そこで
と書き直せば, 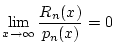 ということも容易にわかるでしょう. これらのことを一般化すると漸近展開という考えになります. ということも容易にわかるでしょう. これらのことを一般化すると漸近展開という考えになります.
ランダウの記号
関数の極限などを考える際に, 慣れてくると発散や収束の優劣という感じのものが見えてきます. 例えば明らかに 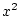 と と 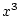 では では 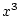 のほうがそのスピードが優ります. このようなときに のほうがそのスピードが優ります. このようなときに 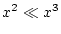 と書くことにしましょう. そしてこういうことは少し考えれば, と書くことにしましょう. そしてこういうことは少し考えれば, 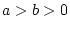 に対して に対して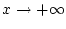 のときに のときに
などとわかります.
さて, いま 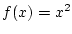 と と 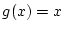 の の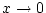 での極限を考えます. 明らかに での極限を考えます. 明らかに 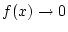 , ,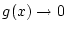 ですがここでこの2つの無限小に関しての比較を考えるとどうでしょうか?直感的には ですがここでこの2つの無限小に関しての比較を考えるとどうでしょうか?直感的には 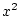 のほうが速く 0 に近づく感じがします. このような感覚を養うことは大切なことです. のほうが速く 0 に近づく感じがします. このような感覚を養うことは大切なことです.
翻って, 唐突ですが, ある狭い範囲での関数の様子を知るために, 記号を使うことにします.
点 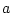 の近くで定義された の近くで定義された 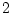 つの関数 つの関数 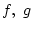 に対して に対して
であるときにこれを
と書くことにします. ここで 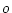 はランダウの記号と呼ばれ, スモールオーと読みます. これは はランダウの記号と呼ばれ, スモールオーと読みます. これは 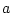 の近くでは の近くでは 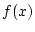 が が 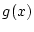 よりもかなり小さいことを意味しています. 特に よりもかなり小さいことを意味しています. 特に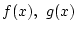 が共に無限小であるときには が共に無限小であるときには 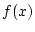 は は 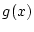 よりも高次(高位)の無限小と呼びます. こちらの言葉はイメージをつかみやすいと思います. よりも高次(高位)の無限小と呼びます. こちらの言葉はイメージをつかみやすいと思います.
以下では特に重要な 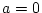 のときの例を示します. のときの例を示します.
例 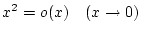
このことは定義より明らか.
例 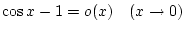
このことは
となることから容易にわかります.
exercise.1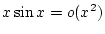 を確かめましょう. を確かめましょう.
次に 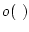 を用いて を用いて 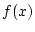 の評価式をつくります. いま の評価式をつくります. いま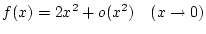 という式の意味ですが, これは という式の意味ですが, これは
ということを意味します. これを言葉で説明するのはなかなか難しいですが, 要するに 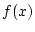 が が 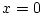 の付近では の付近では 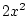 の値に近いことを表しています. 先の例をあらためて観れば の値に近いことを表しています. 先の例をあらためて観れば
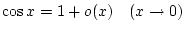 ,と評価されていることになりますから, ,と評価されていることになりますから, 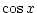 は は 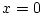 の付近で の付近で 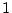 に近いということを意味しています. に近いということを意味しています.
ランダウの記号の性質
ランダウの記号の現れる等式はあくまでも評価式であることに注意しましょう. 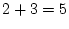 などの通常の等式は両辺が値としてそのものが等しいということですが, ここでは左辺が右辺で評価された等式です. そういうことを踏まえた上で以下の性質について検証します. などの通常の等式は両辺が値としてそのものが等しいということですが, ここでは左辺が右辺で評価された等式です. そういうことを踏まえた上で以下の性質について検証します.
(1) 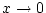 のときに のときに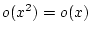 が成り立つ. が成り立つ.
(2) 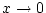 のときに のときに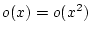 が成り立たない. が成り立たない.
定義に戻って考えて
より (1) の正しいことがわかります. この逆を考えれば, (2) が正しくないことは明らかでしょう.
同様にしていくつかの性質を確かめることができます.
(3) 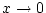 のときに のときに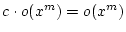 が成り立つ. (c=const) が成り立つ. (c=const)
(4) 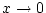 のときに のときに 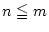 ならば ならば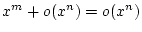 が成り立つ. が成り立つ.
(5) 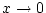 のときに のときに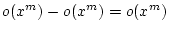 が成り立つ. が成り立つ.
(6) 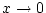 のときに のときに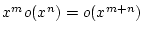 が成り立つ. が成り立つ.
(7) 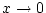 のときに のときに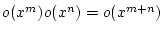 が成り立つ. が成り立つ.
(8) 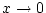 のときに のときに 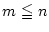 ならば ならば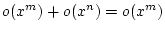 が成り立つ. が成り立つ.
exercise.2 (3)〜(8)を確かめましょう.
ランダウの記号を含む式の計算 先の性質を踏まえて, 式の計算をしてみましょう.
例 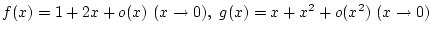 のとき のとき
例 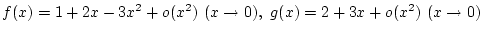 のとき のとき
漸近展開
関数 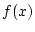 に対して に対して 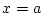 の近くで定義された関数列 の近くで定義された関数列
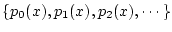 があって があって
となるとき 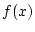 は漸近展開されるといいます. ただしあまりにも一般的だとわかりにくいので少し限定して進めます. は漸近展開されるといいます. ただしあまりにも一般的だとわかりにくいので少し限定して進めます.
関数 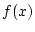 のマクローリン展開 のマクローリン展開
について, これを有限項で打ち切ったものを有限マクローリン展開と呼びます. このとき正確には, 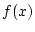 は 0 を含む開区間 は 0 を含む開区間 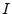 で で 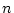 回微分可能なものであるとき 回微分可能なものであるとき 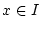 に対して
を満たす に対して
を満たす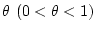 が存在するというのがそれです. ここでの が存在するというのがそれです. ここでの
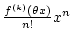 は剰余項と呼ばれているもので, つまり関数の展開を有限で打ち切ったために生ずる誤差の部分を表しています. そしていま, この剰余項の部分をランダウの記号で置き換えたものを関数の漸近展開と呼びます. は剰余項と呼ばれているもので, つまり関数の展開を有限で打ち切ったために生ずる誤差の部分を表しています. そしていま, この剰余項の部分をランダウの記号で置き換えたものを関数の漸近展開と呼びます.
つまり, 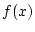 は 0 を含む開区間で は 0 を含む開区間で 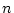 回微分可能なものであるとき 回微分可能なものであるとき
を漸近展開と呼びます.
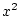 の項までをとった漸近展開の例を以下に示します. ( の項までをとった漸近展開の例を以下に示します. (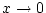 ) )
(1) 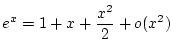
(2) 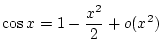
(3) 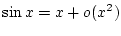
(4) 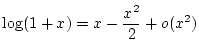
(5) 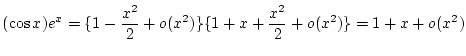
特に (5) では2つの関数の積の漸近展開が漸近展開の積で表されている点に留意します.この性質は本当はしっかり示さなくてはいけません.
exercise.3 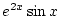 の漸近展開を の漸近展開を 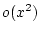 を用いて表しましょう. を用いて表しましょう.
漸近展開の応用
関数の極限
漸近展開の応用として, 関数の極限を求めてみましょう.
問題 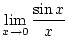 を求めます. を求めます.
解答
問題 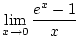 を求めます. を求めます.
解答
この例では 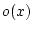 を用いた漸近展開となっていますが, 極限を求める際には問題に応じて展開の項を考える必要があります. また, 上記のような不定形の極限を求めるにはロピタルの定理が有用であることはあらためて指摘するまでもありません. ここではあくまでも漸近展開を使っても極限が求められるということを紹介しました. ただし, どこまでの漸近展開が必要かはわからないところがこれの喰えないところでもあります. を用いた漸近展開となっていますが, 極限を求める際には問題に応じて展開の項を考える必要があります. また, 上記のような不定形の極限を求めるにはロピタルの定理が有用であることはあらためて指摘するまでもありません. ここではあくまでも漸近展開を使っても極限が求められるということを紹介しました. ただし, どこまでの漸近展開が必要かはわからないところがこれの喰えないところでもあります.
exercise.4 以下の関数の極限を漸近展開を用いて求めましょう.
(1) 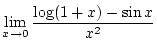
おまけ(漸近線)
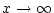 を考えることにして を考えることにして
ですから双曲線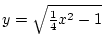 の漸近線が の漸近線が 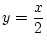 で与えられることがわかります. で与えられることがわかります.
同様にして
より双曲線 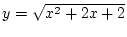 の漸近線が の漸近線が 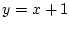 であることも知れます. であることも知れます.
さらには
ですからこの双曲線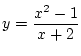 の漸近線のひとつが の漸近線のひとつが 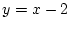 であることがわかります. もちろんのことですがこのあとの展開はそれぞれ高位の無限小の項が続きます. であることがわかります. もちろんのことですがこのあとの展開はそれぞれ高位の無限小の項が続きます.
漸近線と漸近展開を無理矢理結びつけたような話しで恐縮ですが, 実際に使えるので掲げておきました. これらの場合の関数の展開は面倒なので適当なソフトウェア、例えばMathmeticaなどを利用すると良いでしょう. 例えば最後の式の展開は Series[(x^2-1)/(x+2),{x,Infinity,3}] でいける筈です.
あとがき
内容的には大学初年のあたりの教材なのでしょうが, かつてもうだいぶ前に雑誌「数学セミナー」で漸近展開の記事が掲載されていた記憶があります. ここ数年, 極限に触れるときには収束や発散のスピードという話をします. 無限小などの比較の話は直感的な理解で十分で, 決して難しくないと考えています. 今回参考書としてあげた文献の漸近展開の部分を主としてまとめてみました. 内容的にはその参考書の域を出ないばかりか, 正確さを欠く表現もあり, 心苦しいのですが, この点は浅学の故お許し下さい. 一応レベルに配慮して再構成した積もりです. 本来ならばランダウの記号は2つあるわけですが, もう一つのほうは完全に省略しています. また, 有限マクローリン展開に限定したことや, さらには 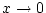 の話だけというのもケチな話です. このあたりの不完全さも重ねてお許し願いたいところです. の話だけというのもケチな話です. このあたりの不完全さも重ねてお許し願いたいところです.
漸近展開の魅力は何といっても, 評価式というところにあると思います. そこでは特別なルールはあるものの, 比較的簡単な演算処理で複雑な式が評価できてしまうことではないでしょうか.
この文書はLaTeX2eでタイプセットしたものをlatex2htmlでHTMLに変換したものです. 若干のレイアウトは修正してありますが本質的にはそれに依存しています.
参考文献
入門微分積分 三宅敏恒 著 培風館
INAX
平成14年10月24日
|