2次関数についての3時間目の授業が終了後すぐ、情報処理室で、コンピューター操作や授業内容についてのアンケートを実施した。このアンケートからは、
・生徒は、我々が予想したほどコンピューターの操作に慣れていなかった。
(生徒:いちいち操作方法がわからず苦労した。そして良くわからなかった。)
・コンピューター操作について個人差があるので、時間は充分すぎるくらい取る必要がある。
(生徒:時間が短かったので、最後までいけなかったのが残念だった。)
・情報処理室が限られた時間しか使えないため、1時間でやる内容を多くしすぎ、生徒を混乱させた。
生徒:画像を見れて良かったけれど、時間がなくて、早くやったのでどれが何だかわからなくなってしまった。
・教材内容や授業の進め方に反省すべき点が多い。
y=a(x-p)2+q より y=ax2+bx+cのほうが、係数とグラフの形や位置の関係がわかりやすいと答えた生徒が多かった。
y=a(x-p)2+q・・・・33.9%
y=ax2+bx+c・・・・66.1%
・おもしろい、楽しいと言う生徒もいたが、コンピューターを操作すること自体が楽しかったという生徒も相当いたと予想される。
といった、反省すべき点や次年度の授業へ向けて改善しなければならない点など、次年度の実践へ向けての貴重な資料を得ることができた。
アンケートとその集計結果は次ページのとおりである。
授業についてのアンケート H7.6.19実施
回答数:男子55名 女子69名 計124名
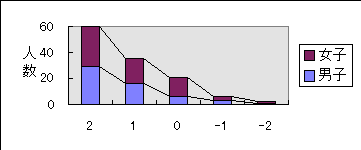
 1.自分の思うようにコンピューターが操作できましたか。
1.自分の思うようにコンピューターが操作できましたか。

|
2 |
1 |
0 |
-1 |
-2 |
| 全体 |
60
|
35
|
21
|
6
|
2
|
| 男子 |
29
|
16
|
6
|
3
|
1
|
| 女子 |
31
|
19
|
15
|
3
|
1
|
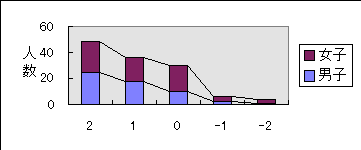
 2.2次関数の方程式の係数a,b,cやa,p,qを変化させると、2次関数のグラフの形や位置が変化することがわかりましたか。
2.2次関数の方程式の係数a,b,cやa,p,qを変化させると、2次関数のグラフの形や位置が変化することがわかりましたか。

|
2 |
1 |
0 |
-1 |
-2 |
| 全体 |
48
|
36
|
30
|
6
|
4
|
| 男子 |
24
|
18
|
10
|
2
|
1
|
| 女子 |
24
|
18
|
20
|
4
|
3
|
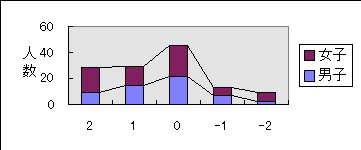
 3.y=ax2+bx+c の係数a,b,cとグラフの形や位置の関係がわかりましたか。
3.y=ax2+bx+c の係数a,b,cとグラフの形や位置の関係がわかりましたか。

|
2 |
1 |
0 |
-1 |
-2 |
| 全体 |
28
|
29
|
45
|
13
|
9
|
| 男子 |
9
|
15
|
22
|
7
|
2
|
| 女子 |
19
|
14
|
23
|
6
|
7
|
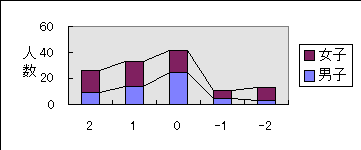
 4.y=a(x-p)2+q の係数a,p,qとグラフの形や位置の関係がわかりましたか。
4.y=a(x-p)2+q の係数a,p,qとグラフの形や位置の関係がわかりましたか。

|
2 |
1 |
0 |
-1 |
-2 |
| 全体 |
26
|
33
|
41
|
11
|
13
|
| 男子 |
9
|
14
|
24
|
5
|
3
|
| 女子 |
17
|
19
|
17
|
6
|
10
|
 5.y=ax2+bx+c と y=a(x-p)2+q
では、どちらの方が関数の方程式からグラフの形や位置をイメージしやすいですか。
5.y=ax2+bx+c と y=a(x-p)2+q
では、どちらの方が関数の方程式からグラフの形や位置をイメージしやすいですか。
ア.y=ax2+bx+c
イ.y=a(x-p)2+q
|
ア |
イ |
| 全体 |
82
|
42
|
| 男子 |
40
|
15
|
| 女子 |
42
|
27
|
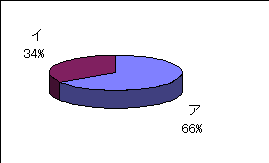
 6.今日の授業の感想を書いてください。
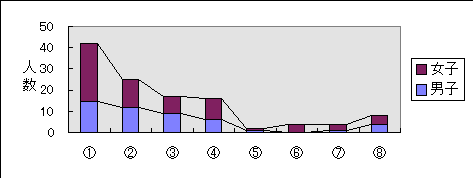
6.今日の授業の感想を書いてください。
< 記 述 内 容 の 分 類>
|
①楽しかった |
②面白かった |
③分かりやすかった |
④またやりたい |
⑤楽しくなかった |
⑥むずかしかった |
⑦分からなかった |
⑧時間が足りない |
| 全体 |
42
|
25
|
17
|
16
|
2
|
4
|
4
|
8
|
| 男子 |
15
|
12
|
9
|
6
|
1
|
0
|
1
|
4
|
| 女子 |
27
|
13
|
8
|
10
|
1
|
4
|
3
|
4
|
< 記 述 内 容 > -原文のまま記載-
- 男 子 -
・個人で操作できて良かった。
・普通の授業よりはグラフの移動がわかりやすかった。
・おもしろかったけれど1人1台コンピューターを使いたかった。
・実際にグラフを動かしてみて、関数の働きが良くわかった。
・コンピューター数学をやるのは初めてだったので、新鮮だった。
・変化が良くわかり楽しくできた。
・2次関数のグラフの形や位置の変化がわかりやすかった。
・授業とは違う楽しみがあった。
・画像を見れて良かったけれど、時間がなくて、早くやったのでどれが何だかわからなくなってしまった。
・コンピューターをもっといろいろな教科で使ってほしい。
・時間が短かったので、最後までいけなかったのが残念だった。
・最後までできなかった。
・正直に言うと普通の授業の方がわかるんじゃないかと思った。
(この生徒は、コンピューターは思うように操作できなかったと記入している)
・おもしろくない。
・処理速度はともかく、拡張性に問題があるのではないか。
- 女 子 -
・できるだけ早くやっていたつもりだったが最後までできなかった。
・1つ1つ良く理解できなかったけれど、何となく形や位置がわかりました。
・言葉で説明されてもわからなかっただろう。
・コンピューターでやった方がおもしろくて数学に興味が分けるような気がした。
・いろいろできて楽しかった。スピーディーにできたらもっと良かったと思う。
・普通の授業よりも理解しやすくておもしろかった。
・コンピューターでグラフをやったりするのは初めてだったのでおもしろかった。
・グラフのイメージがしやすかった。
・良くわかったようなわかんないような気がした。
・いちいち操作方法がわからず苦労した。そして良くわからなかった。
・もうやりたくない。
 授業についてのアンケート
授業についてのアンケート
 1.自分の思うようにコンピューターが操作できましたか。
1.自分の思うようにコンピューターが操作できましたか。

 2.2次関数の方程式の係数a,b,cやa,p,qを変化させると、2次関数のグラフの形や位置が変化することがわかりましたか。
2.2次関数の方程式の係数a,b,cやa,p,qを変化させると、2次関数のグラフの形や位置が変化することがわかりましたか。

 3.y=ax2+bx+c の係数a,b,cとグラフの形や位置の関係がわかりましたか。
3.y=ax2+bx+c の係数a,b,cとグラフの形や位置の関係がわかりましたか。

 4.y=a(x-p)2+q の係数a,p,qとグラフの形や位置の関係がわかりましたか。
4.y=a(x-p)2+q の係数a,p,qとグラフの形や位置の関係がわかりましたか。

 5.y=ax2+bx+c と y=a(x-p)2+q
では、どちらの方が関数の方程式からグラフの形や位置をイメージしやすいですか。
5.y=ax2+bx+c と y=a(x-p)2+q
では、どちらの方が関数の方程式からグラフの形や位置をイメージしやすいですか。
 6.今日の授業の感想を書いてください。
6.今日の授業の感想を書いてください。