 娭悢儔儃傪梡偄偨庼嬈偵偮偄偰
娭悢儔儃傪梡偄偨庼嬈偵偮偄偰
丂偙傟傑偱俀師娭悢偺僌儔僼偺巜摫偼丄僾儕儞僩傪巊梡偟偰丄倶偲倷偺娫偺懳墳昞傪偮偔傝丄嵗昗暯柺忋偵揰傪庢偭偰僌儔僼傪彂偒偦偺宍傗埵抲娭學傪挷傋偨傝偟偰巜摫偟偰偄偨丅傕偪傠傫丄揰傪寢傇偲曻暔慄偵側傞帠傪懱尡偝偣傞偙偲偼丄幚嵺偵僌儔僼傪彂偔帪偵栶棫偪丄崱屻偺戙悢揑側埖偄偵傛傞拪徾揑側妛廗偺棟夝偺彆偗偵傕側傞偱偁傠偆丅
丂偟偐偟丄偙偆偄偭偨巜摫偱偼丄椺偊偽丄倷亖倶俀偺僌儔僼傪倶幉曽岦偵俁丆倷幉曽岦偵俀堏摦偡傞偲倷亖(倶亅俁)俀亄俀偺僌儔僼偵廳側傞帠側偳偼丄捀揰偺堏摦側偳偐傜棟榑揑偵偼擺摼偝偣傞偙偲偼偱偒傞偩傠偆偑丄偼偭偒傝偲僀儊乕僕傪帩偨偣傞帠偼擄偟偄丅僐儞僺儏乕僞乕偺夋柺偵條乆偺僌儔僼傪昞帵偟偨傝幚嵺偵僌儔僼傪堏摦偝偣偰尒偣傞偙偲偵傛傝丄栤戣堄幆傗嫽枴傪堷偒偍偙偟丄崱屻偺妛廗傊偺摦婡晅偗偵傕偟偨偄丅傑偨丄懳墳昞偐傜揰傪庢傝僌儔僼傪彂偔偵偼懡偔偺帪娫傪昁梫偲偡傞丅僐儞僺儏乕僞乕偱僌儔僼傪昤偄偰尒偣傞偙偲偵傛傝帪娫傪愡栺偱偒丄偦偺暘墘廗偵椡傪擖傟偨偄偲峫偊偨丅
丂偙偙偱偼丄僐儞僺儏乕僞乕偵傛傞庼嬈傪峴偭偨俁僋儔僗偺偆偪丄侾擭俇慻偺椺傪師儁乕僕偐傜徯夘偡傞丅
丂俀師娭悢偱偼丄娭悢偺掕媊堟傗抣堟丆俀師娭悢偺學悢偲僌儔僼偺宍傗埵抲偺娭學偺巜摫偵丄俀帪娫僐儞僺儏乕僞乕傪巊梡偟偨丅傑偨丄俀師娭悢偺僌儔僼偲倶幉偺埵抲娭學偺墘廗丂栤戣傪僐儞僺儏乕僞乕傪梡偄偰巜摫偟偨丅僜僼僩偼娭悢儔儃偱偁傞丅
仢俇寧侾俆擔(栘)丂亅俀師娭悢侾帪娫栚亅
仢俇寧侾俇擔(嬥)丂亅俀師娭悢俀帪娫栚(亄悢妛俙偺帋尡)亅
仢俇寧侾俋擔(寧)丂亅俀師娭悢俁帪娫栚亅
丂傑偨丄偙偺庼嬈廔椆屻偵傾儞働乕僩傪幚巤偟偨丅侾俇儁乕僕偐傜傾儞働乕僩偺廤寁寢壥傪婰嵹偟偰偄傞丅
仢俉寧俀俉擔(寧) 亅俀師娭悢俀侽帪娫栚亅
![]() 侾.僐儞僺儏乕僞乕偵傛傞巜摫偺幚巤奣嫷(侾擭俇慻)
侾.僐儞僺儏乕僞乕偵傛傞巜摫偺幚巤奣嫷(侾擭俇慻)
俀師娭悢偺嵟弶偺帪娫偱丄
丂丂丂丂戞侾復 俀師娭悢 丂侾.娭悢偲僌儔僼
丂丂丂丂丂丂娭悢儔儃偺憖嶌偺巇曽丂丂丂娭悢偺掕媊丂丂丂掕媊堟丂丂丂抣堟丂
丂丂丂丂丂侾師娭悢偺僌儔僼丂丂丂丂丂侾師娭悢偺掕媊堟,抣堟
傪忣曬張棟幒偱僐儞僺儏乕僞乕傪巊梡偟偰巜摫偟偨
娭悢儔儃偺僼傽僀儖偺撪梕傪俋儁乕僕偐傜婰嵹偟偰偄傞丅
忣曬張棟幒偑巊偊側偄偨傔丄侾擭俇慻嫵幒偵偍偄偰係侽暘娫偱慜偺扨尦(悢妛俙丗戞侾復
悢偲幃丂戞俁愡 幃偲徹柧)偺傑偲傔偺帋尡傪幚巤丅
丂侾侽暘娫偱丄
丂丂丂戞侾復 俀師娭悢 丂俀.娭悢偲僌儔僼
俀師娭悢偺掕媊丂丂丂忋偵撌,壓偵撌
丂丂丂倷亖倶俀,倷亖亅倶俀
偺僌儔僼丂丂丂曻暔慄丂丂丂捀揰,幉
偵偮偄偰娙扨偵愢柧偟偨丅晛捠嫵幒側偺偱僐儞僺儏乕僞乕偼巊梡偟偰偄側偄丅
丂忣曬張棟幒偱僐儞僺儏乕僞乕傪巊梡偟偰丄
丂丂丂丂戞侾復 俀師娭悢 丂俀.娭悢偲僌儔僼
丂丂丂丂丂丂y=ax俀丆y=ax俀+bx+c丆y=a(x-倫)俀+q
偺學悢偲僌儔僼偺宍傗埵抲偺娭學
丂丂丂丂丂丂僌儔僼偺捀揰偲幉
偵偮偄偰巜摫偟偨丅
丂娭悢儔儃偺僼傽僀儖偺撪梕傪侾俀儁乕僕偵丄妛廗巜摫埬傪侾俁丆侾係儁乕僕偵丄庼嬈偱梡偄偨僾儕儞僩傪侾俆儁乕僕偵婰嵹偟偰偄傞丅
丂忣曬張棟幒偱僐儞僺儏乕僞乕傪巊梡偟偰丄
丂丂丂丂戞侾復 俀師娭悢 丂俆.俀師曽掱幃
偱丄俀師娭悢偺僌儔僼偲倶幉偺埵抲娭學偵娭偡傞墘廗栤戣丄椺戣係,楙廗俀侾,椺戣俆,楙廗俀俀傪巜摫偟偨丅僐儞僺儏乕僞乕傪巊梡偡傞偙偲偵傛傝丄寁嶼偩偗偱廔傢傜偢偵忢偵僌儔僼偺僀儊乕僕傪帩偨偣側偑傜巜摫偱偒偨丅
![]() 俀.俀師娭悢侾帪娫栚偺庼嬈偵巊梡偟偨娭悢儔儃僼傽僀儖
(俇寧侾俆擔幚巤暘)
俀.俀師娭悢侾帪娫栚偺庼嬈偵巊梡偟偨娭悢儔儃僼傽僀儖
(俇寧侾俆擔幚巤暘)
乭娭悢摫擖.LMS乭
丒懳徾幃 (a,f(a))
丒掕媊幃 f(x)=x俀
丒婰丂榐
娭悢偼丄拞妛峑偱傕妛廗偟偰偒傑偟偨偹丅
拞妛峑偱偼偳傫側娭悢傪妛廗偟傑偟偨偐丠丂妛廗偟偨娭悢傪侾偮尵偭偰偔偩偝偄丅
倷亖丂丂丂丂丂丂ゥ@
丂丂丂僷僜僐儞偑嘆偺僌儔僼傪彂偄偰偔傟傑偡丅椙偔尒偰偄偰偔偩偝偄丅
丂丂丂丂丂丂亅偦偙偱幙栤亅
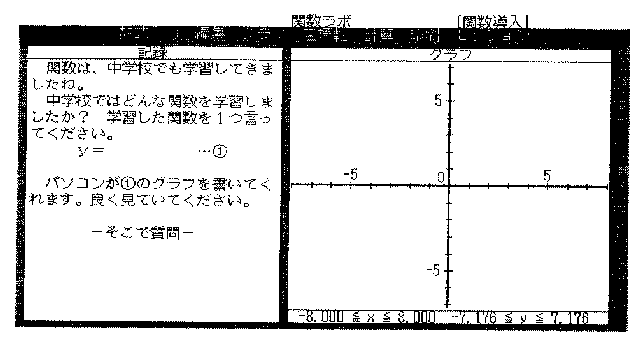
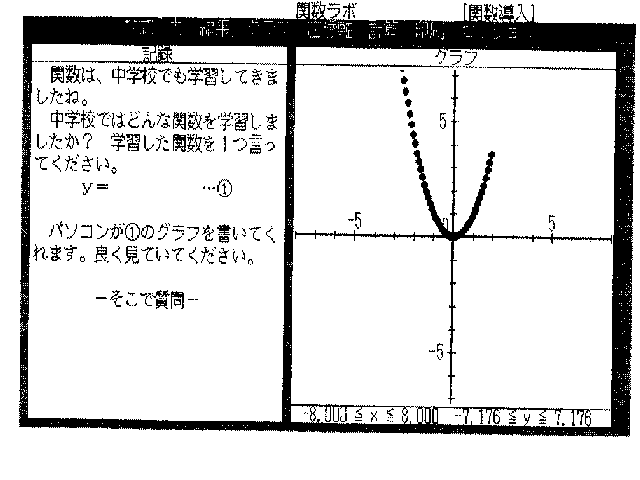
乭曄悢侾.LMS乭
丒懳徾幃 y=f(x) (a,0)-(a,f(a))-(0,f(a)) (a,f(a)) (a,0) (0,f(a))
丒掕媊幃 f(x)=2x+1
丒婰丂榐
<柾媅帋尡庴尡幰偲庴尡椏>
戞俀夞柾帋(庴尡椏2300墌)偵偮偄偰丄
庴丂尡丂幰 仺 倶恖 庴尡椏憤妟 仺 倷墌
丂丂 偲偡傞偲偒丄倶偲倷偺娫偵
丂丂 倶 倷
俀恖亅亅亅仺 4600墌
俆恖亅亅亅仺11500墌
丂丂 偲偄偭偨懳墳偑偁傞丅
丂丂 偙偺偲偒丄倶偲倷偼曄壔偡傞検偺偄傠偄傠側抣傪戙昞偟偰偄傞丅

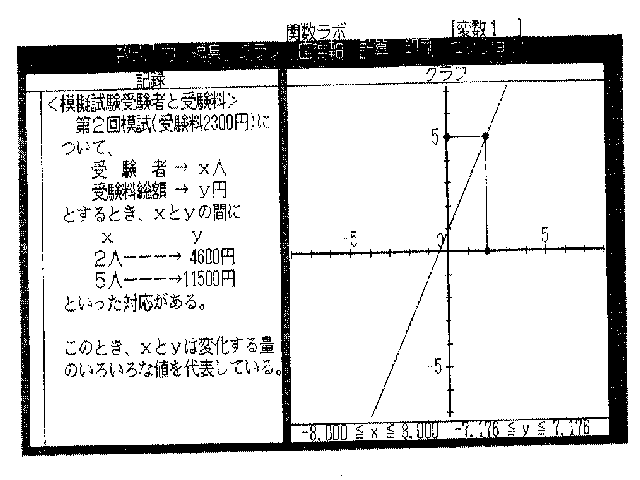
乭娭悢掕媊.LMS乭
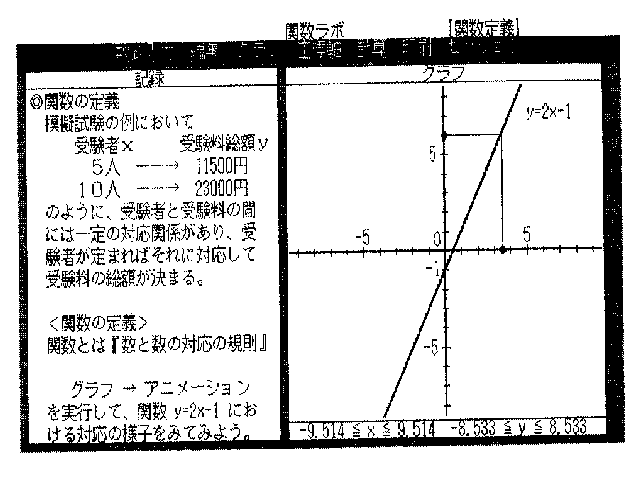
丒僌儔僼 偁傜偐偠傔y=2x-1偺僌儔僼偑昤偐傟偰偄傞丅
丒懳徾幃丂丂(a,0)-(a,f(a))-(0,f(a)) (a,0) (0,f(a))
丒掕媊幃 f(x)=2x-1
丒婰丂榐
仢娭悢偺掕媊
柾媅帋尡偺椺偵偍偄偰
庴尡幰倶 庴尡椏憤妟倷
俆恖丂亅亅仺丂11500墌
侾侽恖丂亅亅仺丂23000墌
偺傛偆偵丄庴尡幰偲庴尡椏偺娫偵偼堦掕偺懳墳娭學偑偁傝丄庴
尡幰偑掕傑傟偽偦傟偵懳墳偟偰庴尡椏偺憤妟偑寛傑傞丅
丂丂 亙娭悢偺掕媊亜
娭悢偲偼亀悢偲悢偺懳墳偺婯懃亁
丂丂 丂 僌儔僼仺傾僯儊乕僔儑儞
丂丂 傪幚峴偟偰丄娭悢 y=2x-1 偵偍 偗傞懳墳偺條巕傪傒偰傒傛偆丅
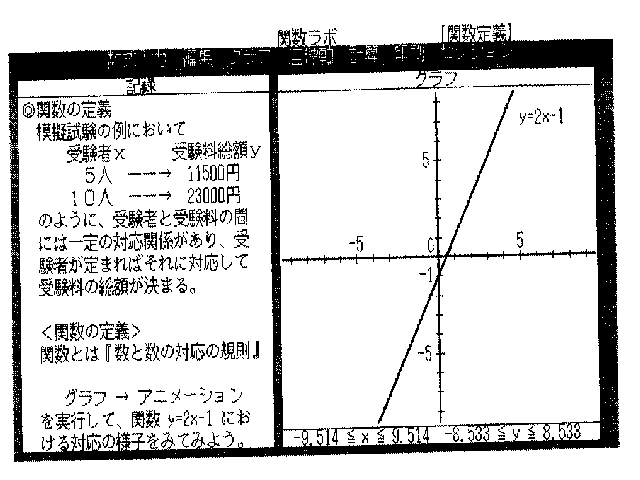
乭掕丒抣堟.LMS乭
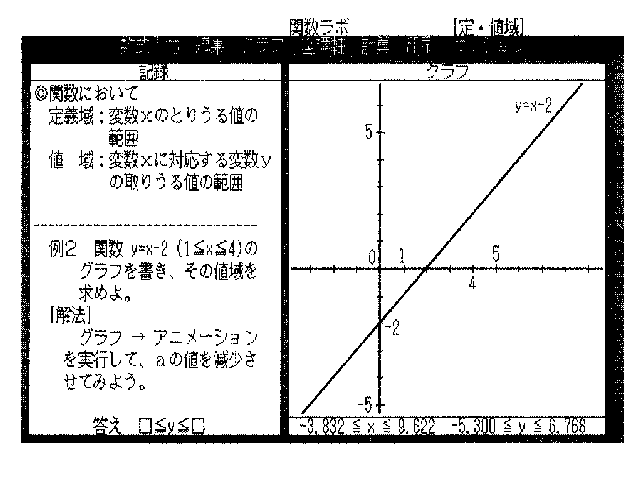
丒僌儔僼 偁傜偐偠傔y=x-2偺僌儔僼偑昤偐傟偰偄傞丅
丒懳徾幃丂丂y=f(x)丂丂(1+a,0)-(1+a,f(1+a))-(0,f(1+a)) (0,f(1+a))
丒掕媊幃 f(x)=x-2
丒婰丂榐
仢娭悢偵偍偄偰
掕媊堟丗曄悢倶偺偲傝偆傞抣偺斖埻
丂丂 抣 堟丗曄悢倶偵懳墳偡傞曄悢倷偺庢傝偆傞抣偺斖埻
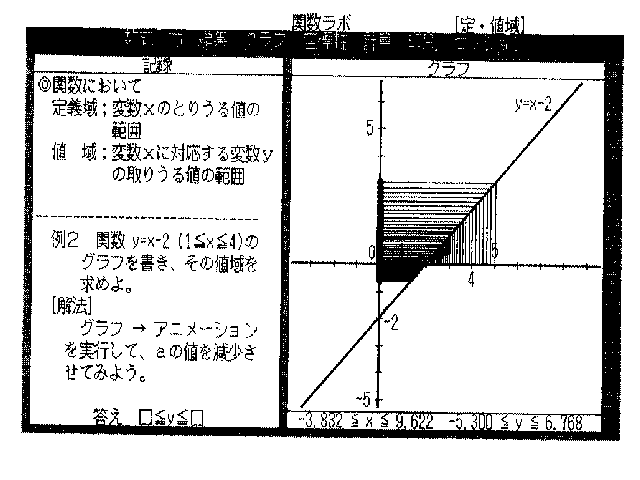
椺俀丂娭悢 y=x-2 (1亝x亝4)偺僌儔僼傪彂偒丄偦偺抣堟傪媮傔傛丅
[夝朄] 僌儔僼仺傾僯儊乕僔儑儞傪幚峴偟偰丄倎偺抣傪尭彮偝偣偰傒傛偆丅
摎偊丂仩亝y亝仩
乭楙俀(1).LMS乭
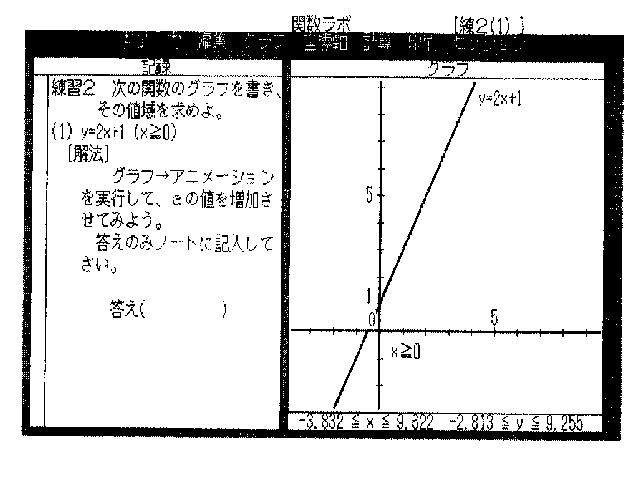
丒僌儔僼 偁傜偐偠傔y=2x+1偺僌儔僼偑昤偐傟偰偄傞丅
丒懳徾幃丂丂y=f(x)丂丂(0+a,0)-(0+a,f(0+a))-(0,f(0+a)) (0,f(0+a))
丒掕媊幃 f(x)=2x+1
丒婰丂榐
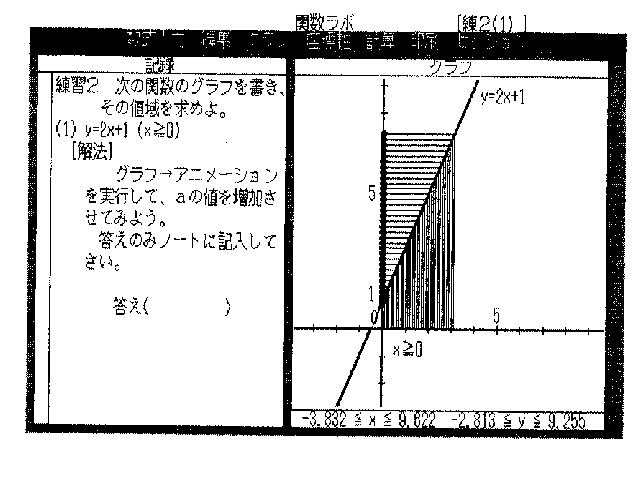
楙廗俀丂師偺娭悢偺僌儔僼傪彂偒丄偦偺抣堟傪媮傔傛丅
(1) y=2x+1 (x亞0)
[夝朄] 僌儔僼仺傾僯儊乕僔儑儞傪幚峴偟偰丄倎偺抣傪憹壛偝偣偰傒傛偆丅
摎偊偺傒僲乕僩偵婰擖偟偰偔偩偝偄丅
乭楙俀(2).LMS乭
丒僌儔僼 偁傜偐偠傔y=-3x+2偺僌儔僼偑昤偐傟偰偄傞丅
丒懳徾幃丂丂y=f(x)丂丂(-2+a,0)-(-2+a,f(-2+a))-(0,f(-2+a)) (0,f(-2+a))
丒掕媊幃 f(x)=-3x+2
丒婰丂榐
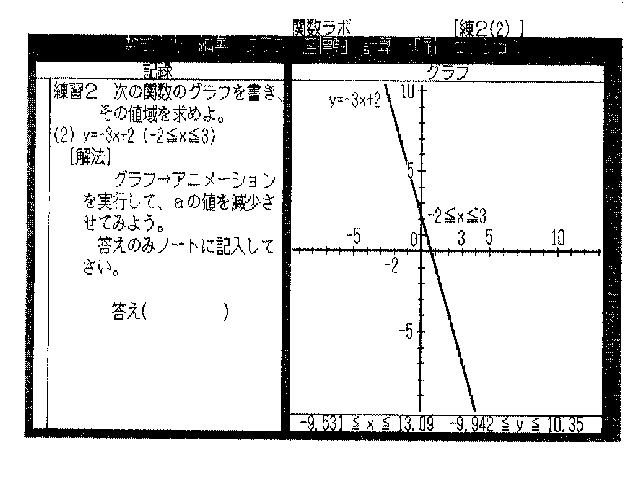
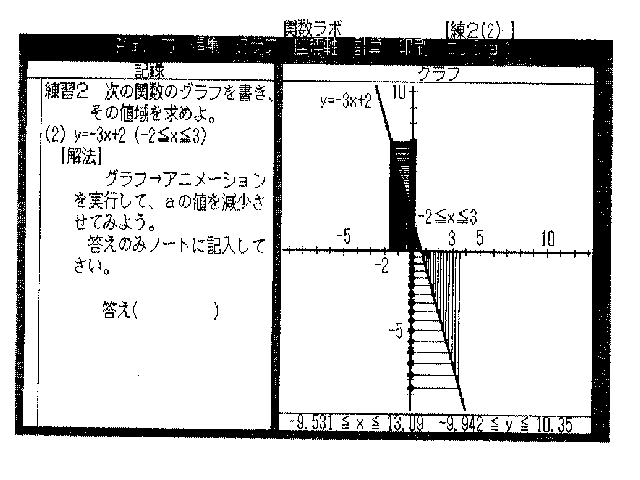
楙廗俀丂師偺娭悢偺僌儔僼傪彂偒丄偦偺抣堟傪媮傔傛丅
(2) y=-3x+2 (-2亝x亝3)
[夝朄] 僌儔僼仺傾僯儊乕僔儑儞傪幚峴偟偰丄倎偺抣傪尭彮偝偣偰傒傛偆丅
摎偊偺傒僲乕僩偵婰擖偟偰偔偩偝偄丅
![]() 俁.俀師娭悢俁帪娫栚偺庼嬈偵巊梡偟偨娭悢儔儃僼傽僀儖
(俇寧侾俋擔幚巤暘)
俁.俀師娭悢俁帪娫栚偺庼嬈偵巊梡偟偨娭悢儔儃僼傽僀儖
(俇寧侾俋擔幚巤暘)
乭2師娭悢1.LMS乭
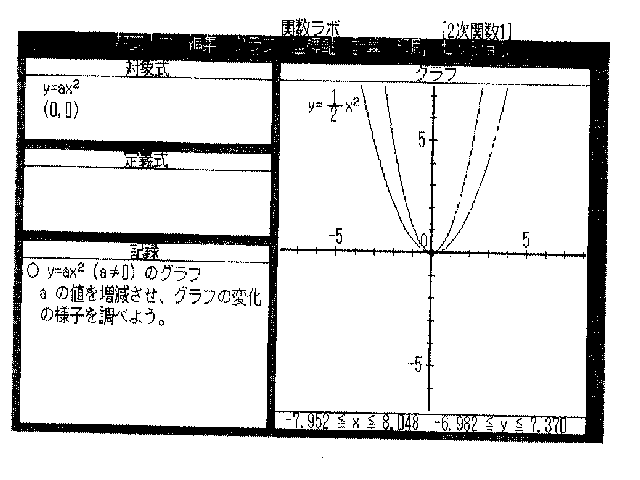
丒僌儔僼丂丂偁傜偐偠傔y=1/2x2偺僌儔僼偑昤偐傟偰偄傞丅
丒懳徾幃 y=ax俀丂丂丂 (0,0)
丒婰丂榐
丂仢俀師娭悢倷亖倎倶俀(a亗0)偺皋滋倎偺抣傪憹尭偝偣丄僌儔僼偺曄壔偺條巕傪挷傋傛偆丅
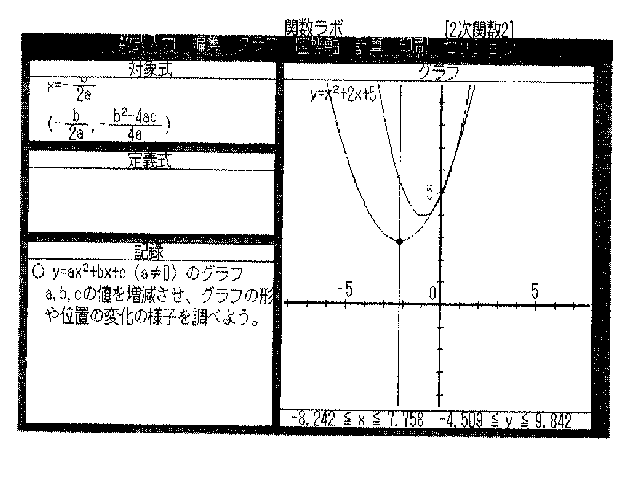
乭2師娭悢2.LMS乭
丒僌儔僼 偁傜偐偠傔倷亖倶俀亄俀倶亄俆偺僌儔僼偑昤偐傟偰偄傞丅
丒懳徾幃 y=ax俀+bx+c丂丂丂x=-b/2a丂丂丂(-b/2a丆-(b2-4ac)/4a)
丒婰丂榐
丂 仢俀師娭悢y=ax俀+bx+c(a亗0)偺皋滋
倎,倐,們偺抣傪憹尭偝偣丄僌儔僼偺宍傗埵抲偺曄壔偺條巕傪挷傋傛偆丅
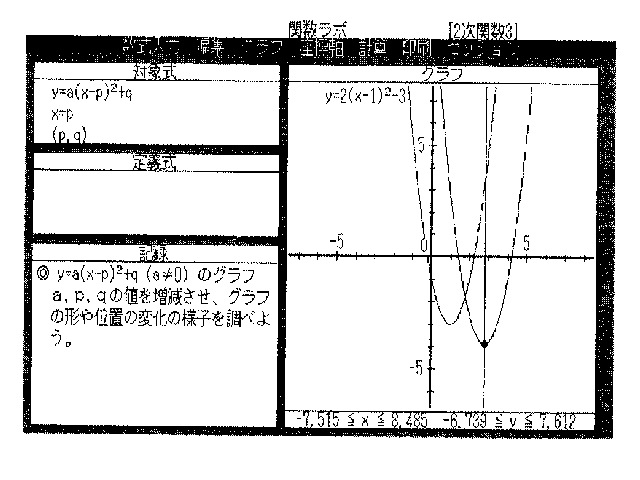
乭2師娭悢3.LMS乭
丒僌儔僼 偁傜偐偠傔丂倷亖俀(倶亅侾)俀亅俁偺僌儔僼偑昤偐傟偰偄傞丅
丒懳徾幃 y=a(x-p)俀+倯 x=p (p,q)
丒婰丂榐
仢俀師娭悢y=a(x-p)俀+倯(a亗0)偺皋滋
倎,倫,倯偺抣傪憹尭偝偣丄僌儔僼偺宍傗埵抲偺曄壔偺條巕傪挷傋傛偆丅
![]() 係.俀師娭悢俁帪娫栚偺庼嬈偺妛廗巜摫埬
(俇寧侾俋擔幚巤)
係.俀師娭悢俁帪娫栚偺庼嬈偺妛廗巜摫埬
(俇寧侾俋擔幚巤)
![]() 俆.俀師娭悢俁帪娫栚偺庼嬈偵巊梡偟偨僾儕儞僩
(俇寧侾俋擔巊梡)
俆.俀師娭悢俁帪娫栚偺庼嬈偵巊梡偟偨僾儕儞僩
(俇寧侾俋擔巊梡)