丂丂丂
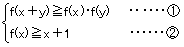
傪枮偨偟偰偄傞丅
丂偙偺偲偒丆師偺奺栤偵摎偊傛丅
| 栤戣暥 |
丂f(倶)偼偡傋偰偺幚悢偱掕媊偝傟偨娭悢偱丆擟堄偺幚悢倶丆倷偵懳偟偰丆
丂丂丂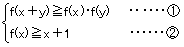
傪枮偨偟偰偄傞丅
丂偙偺偲偒丆師偺奺栤偵摎偊傛丅
| (1) | 倖(0)偺抣傪媮傔傛丅 |
| (2) | 倶亜0偺偲偒丆倖(-倶)亙倖(0)亙倖(倶)傪帵偣丅 |
| (3) | 丂擟堄偺幚悢倶偵懳偟偰丆倖(倶)亜0傪帵偣丅 |
| (4) | 丂倶亙倷偺偲偒丆倖(倶)亙倖(倷)傪帵偣丅 |
| 拝娽揰 |
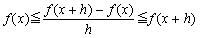
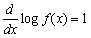
| 夝摎椺 |
| (1) |
嘆偵倶亖倷亖0傪戙擖偟偰丆丂倖(0)亞乷倖(0)乸2 傛偭偰丂0亝倖(0)亝1 嘇偵倶亖0傪戙擖偟偰丆倖(0)亞1 備偊偵丂倖(0)亖1丂丂丂乮摎乯倖(0)亖1 |
| (2) |
倶亜0偺偲偒丆嘇傛傝 丂丂丂倖(倶)亞倶亄1亜1亖倖(0) 傑偨丆嘆傛傝丆 丂丂丂1亖倖(0)亖倖(倶亄(亅倶))亞倖(倶)倖(亅倶) 倖(倶)亜1偱偁偭偨偐傜 丂丂丂倖(亅倶)亝1/倖(倶)亙1亖倖(0) 備偊偵丂倖(-倶)亙倖(0)亙倖(倶)丂丂乮徹柧廔乯 |
| (3) |
嘆傛傝丆 丂丂丂f(倶)=f(倶/2亄倶/2)亞乷f(倶/2)乸2亞0 側偺偱丆f(x)亗0傪帵偣偽傛偄丅 丂攚棟朄偱徹柧偡傞丅 f(倶0)=0側傞幚悢倶0偑懚嵼偡傞偲壖掕偡傞偲丆f(倶0)亞乷倖(倶0/2)乸2傛傝丆f(倶0/2)亖0 摨條偵偟偰丆 丂丂丂f(倶0/2)亞乷f(倶0/4)乸2傛傝丆倖(倶0/4)亖0 偙傟傪孞傝曉偟偰偄偗偽丆 丂丂丂f(倶0/2値)亖0丂乧乧嘊 偑擟堄偺帺慠悢値偵懳偟偰惉傝棫偮偙偲偑傢偐傞丅 堦曽丆嘇偐傜丆 丂丂丂f(倶0/2値)亞倶0/2値亄1 偱偁傞偐傜丆乮2値亜乥倶0乥偲側傞傛偆側乯廫暘戝偒偄帺慠悢値偵懳偟偰偼丆 丂丂丂f(倶0/2値)亜0 偙傟偼丆嘊偵柕弬偡傞丅偟偨偑偭偰丆擟堄偺幚悢倶偵懳偟偰丆 丂丂丂f乮x乯亜0 偑惉傝棫偮丅丂丂丂乮徹柧廔乯 |
| (4) |
倶亙倷偺偲偒丆1亙倖(倷亅倶乯偱偁傞偐傜丆曈乆偵倖(倶)亜0傪偐偗偰丆 丂丂丂倖(倶)亙倖(倷亅倶)倖(倶)亝倖(倷亅倶亄倶)亖倖(倷) 備偊偵丆倖(倶)亙倖(倷)丂丂丂乮徹柧廔乯 |
| 亙(5)偲(6)偺夝摎椺亜 | |
| (5) |
倛亜0偺偲偒 丂丂丂倖(倶亄倛)亞倖(倶)倖(倛)亞倖(倶)(倛亄1)丂丂乮佹(3)乯 丂丂丂丂丂丂丂丂丂丂丂丂丂亖倛倖(倶)亄倖(倶) 偟偨偑偭偰丆 丂丂丂 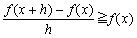 傑偨丆倖(倶)亖倖(倶亄倛亅倛) 丂丂丂丂丂亞倖(倶亄倛)倖(亅倛) 丂丂丂丂丂亞倖(倶亄倛)(亅倛亄1)丂丂乮佹(3)乯 丂丂丂丂丂亖亅倛倖(倶亄倛)亄倖(倶亄倛) 偟偨偑偭偰丆 丂丂丂 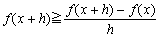 備偊偵丆 丂丂丂 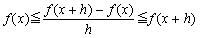 丂丂丂乮徹柧廔乯 丂丂丂乮徹柧廔乯
|
| (6) |
(傾)(5)偺倶傪倶亅倛偵抲偒姺偊傞偙偲偵傛傝丆 丂丂丂 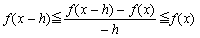 丂偟偨偑偭偰丆倖偑楢懕偱偁傟偽丆(5)偲偼偝傒偆偪偺尨棟偐傜丆 丂丂丂 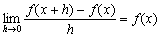 丂偑傢偐傞丅偡側傢偪丆倖偼旝暘壜擻偱丆 丂丂丂倖'(倶)亖倖(倶) 丂偑惉傝棫偮丅丂丂丂乮徹柧廔乯 (僀) 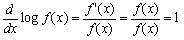 丂丂丂乮徹柧廔乯 丂丂丂乮徹柧廔乯(僂)(僀)傛傝丆log f(倶)亖倶亄俠乮俠偼愊暘掕悢乯 丂倶亖0傪戙擖偡傞偲丆log f(0)亖俠丏傛偭偰俠亖0偲側傝丆 丂丂丂log f(倶)亖倶丂丂亪f(倶)亖倕倶丂丂丂乮徹柧廔乯 |