に対して，Ｎ(α)をＮ(α)＝α2−3ｂ2
と定義する。例えば，Ｎ(3＋2
)＝32−3･22＝−3いま，2つの数の集合
Ａ＝｛α｜α＝ａ＋ｂ
(ａ，ｂは整数)｝Ｂ＝｛α｜αはＡの要素で かつ Ｎ(α)＝1｝
について，次の問に答えよ。
| 問題文 |
ａ，ｂを整数として，ａ＝ａ＋ｂに対して，Ｎ(α)を
Ｎ(α)＝α2−3ｂ2
と定義する。例えば，Ｎ(3＋2)＝32−3･22＝−3
いま，2つの数の集合
Ａ＝｛α｜α＝ａ＋ｂ (ａ，ｂは整数)｝
Ｂ＝｛α｜αはＡの要素で かつ Ｎ(α)＝1｝
について，次の問に答えよ。
| (1) |
Ａの2つの要素α＝ａ＋ｂ，β＝ｃ＋ｄに対して， Ｎ(α･β)＝Ｎ(α)･Ｎ(β) が成り立つことを示せ。
|
| (2) |
Ｕの要素αに対し，α2 および 1/α がＵに属していることを示せ。
|
| (3) |
3ｎ2＋1が平方数（自然数の平方である数）となる自然数ｎが無数にあることを示せ。
|
| 着眼点 |
| (1) |
αβ＝(ａｃ＋3ｂｄ)＋(ａｄ＋ｂｃ) 等式 (ａｃ＋3ｂｄ)2−3(ａｄ＋ｂｃ)2 ＝(ａ2−3ｂ2)(ｃ2−3ｄ2) を示すことになる。 |
| (2) |
(1)より，Ｎ(α2)＝(Ｎ(α))2＝1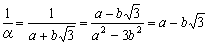 Ｎ(1/α)＝ａ2−3･(−ｂ)2＝ａ2−3ｂ2＝1 |
| (3) |
Ｕの要素の1つとして，2＋＝ωがある。 ω＞1より，ω＜ω2＜ω3＜…＜ωl＜… |
| 解答例 |
| (1) |
αβ＝(ａ＋ｂ)(ｃ＋ｄ) ＝(ａｃ＋3ｂｄ)＋(ａｄ＋ｂｃ) Ｎ(αβ)＝(ａｃ＋3ｂｄ)2−3(ａｄ＋ｂｃ)2 ＝ａ2ｃ2＋6ａｂｃｄ＋9ｂ2ｄ2−3ａ2ｄ2−6ａｂｃｄ−3ｂ2ｃ2 ＝ａ2ｃ2−3ａ2ｄ2−3ｂ2ｃ2＋9ｂ2ｄ2 ＝(ａ2−3ｂ2)(ｃ2−3ｄ2) ＝Ｎ(α)Ｎ(β) （証終）
|
| (2) |
Ｎ(α)＝1だから，(1)より Ｎ(α2)＝(Ｎ(α))2＝1 もちろん，α2∈Ａだから，α2∈Ｕ，α＝ａ＋ｂ とおくと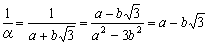， (∵ａ2−3ｂ2＝1)Ｎ(1/α)＝ａ2−3･(−ｂ)2＝ａ2−3ｂ2＝1 1/α∈Ａだから，1/α∈Ａ （証終） |
| (3) |
Ｎ(2＋)＝22−3･12＝1 よって2＋ ∈Ｕいま，2＋ ＝ωとおくと，ω＞1だから，ω＜ω2＜ω3＜ω4＜… で，ωｌ∈Ｕ(ｌ＝1，2，3，…) ωｌ＝ａｌ＋ｂｌ とおくと，Ｎ(ωｌ)＝ａｌ2−3ｂｌ2＝1 ∴3ｂｌ2＋1＝ａｌ2 ωｌ＋1＝ωｌ･ω＝(ａｌ＋ｂｌ )(2＋)＝(2ａｌ＋3ｂｌ)＋(ａｌ＋2ｂｌ) ｂｌ＋1＝ａｌ＋2ｂｌ＞ｂｌ ｂ1＜ｂ2＜ｂ3＜… よって，3ｎ2＋1が平方数となるｎとして，ｂ1，ｂ2，ｂ3，…があるので，無数に存在する。 （証終） |