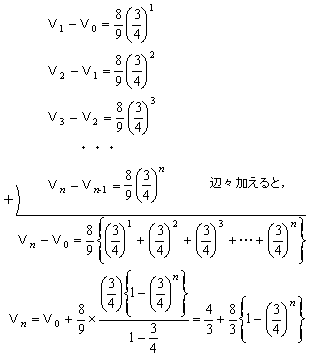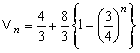| (1) |
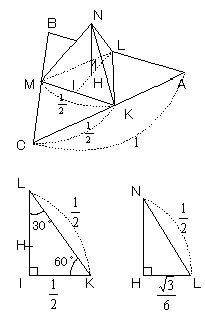 頂点Nから,△KLMへ垂線を下ろした点をHとする。
頂点Nから,△KLMへ垂線を下ろした点をHとする。
床面の△KLMの頂点Lから辺MKへ垂線を下ろした点をIとする。
辺IK=1/4,IK:KL:LI=1:2: より より
KI= /4 /4
また,IH:HL=1:2より
LH= /6 /6
三平方の定理NH2+HL2=NL2より
NH2=1/4-3/36
NH2=1/4-1/12
∴NH=1/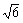
正四面体KLMKの高さは1/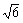 である。 である。
体積をV0とおくと
V0=1/3×△KLM×NH
=1/3×1/2・(1/2)2×sin60°×1/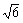
=1/24× /2×1/ /2×1/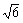
=1/48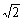
=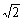 /96 …(答) /96 …(答)
|
| (2) |
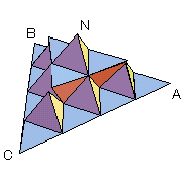 第1段階の図形には,1辺が1/2の正三角形が6個集まったものである。
第1段階の図形には,1辺が1/2の正三角形が6個集まったものである。
前問より1辺の長さが1の正三角形の上に形成される正四面体の高さは1/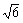 であるから,1辺が1/4の正三角形の上に形成される,正四面体の高さは1/4 であるから,1辺が1/4の正三角形の上に形成される,正四面体の高さは1/4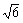
小さな正四面体の体積をW0とすると
W0=1/3×1/2×(1/4)2sin60°×1/4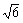
求める体積をV1とおくと,
V1=V0+6×W0
=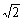 /96+ /96+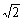 /256=11 /256=11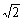 /768 /768
|
| (3) |
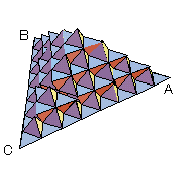 第2段階の図形には,1辺が1/4の正三角形が62(=36)個,集まったものである。
第2段階の図形には,1辺が1/4の正三角形が62(=36)個,集まったものである。
同様にして,1/8の正三角形の上に形成される正四面体の高さは1/8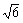
体積をW1とすると,
W1=1/3×1/2・(1/8)2sin60°×1/8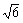
求める体積をV2とおくと
V2=V1+36W1
=11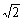 /768+3 /768+3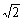 /1024=53 /1024=53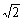 /3072 /3072
|
| (4) |
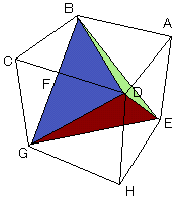 1辺の長さが2の立方体より,AB=AD=2
1辺の長さが2の立方体より,AB=AD=2
三平方の定理よりBD=2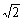
正四面体BDGEは,1辺の長さが2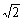 からなる正三角形で形成されている。 からなる正三角形で形成されている。
体積をV0とおくと
V0=1/3×1/2×(2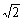 )2×sin60°×2 )2×sin60°×2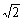 / /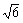
∴V0=4/3
|
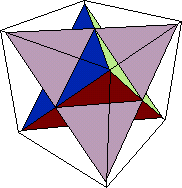 第1段階の操作として,正四面体BDGEの4つの正三角形の上に,1辺の長さが
第1段階の操作として,正四面体BDGEの4つの正三角形の上に,1辺の長さが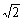 の正四面体を4個加えるので,体積をV1とおくと の正四面体を4個加えるので,体積をV1とおくと
V1=V0+4×1/3×1/2×(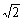 )2sin60°× )2sin60°×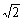 / /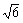
V1=V0+2/3
∴V1=2
|
 第2段階の操作として,第1段階の1辺が
第2段階の操作として,第1段階の1辺が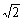 の6×4個の正三角形の上に,1辺が の6×4個の正三角形の上に,1辺が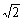 /2の正四面体を6×4個加えるたもので,体積をV2とおくと /2の正四面体を6×4個加えるたもので,体積をV2とおくと
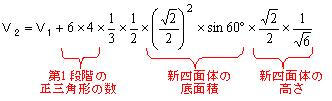
V2=V1+6×4×1/3×1/2×(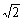 /2)2×sin60°× /2)2×sin60°×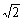 /2×1/ /2×1/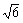
∴V2=5/2
|
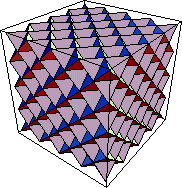 第3段階以降は帰納的に考えられないだろうか。
第3段階以降は帰納的に考えられないだろうか。
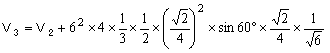
∴V3=23/8
以下同様に考えると
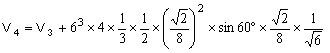
∴V4=23/8+9/32=101/32
V0:V4=4/3:101/32=128:303 …(答)
|
 第n段階の体積Vnと第n-1段階の体積Vn-1との関係式を作成してみる。
第n段階の体積Vnと第n-1段階の体積Vn-1との関係式を作成してみる。
V0=4/3
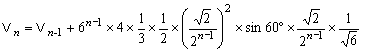
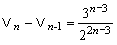 ∴ ∴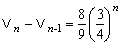 …① …①
①にn=1,2,3,…,nまで代入すると
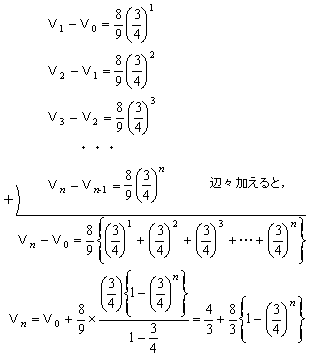
∴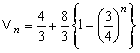
|
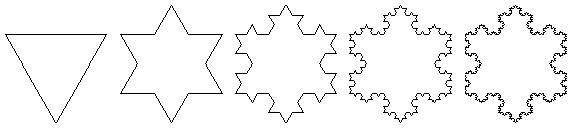
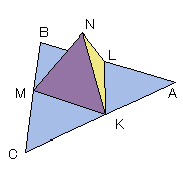 第1段階
第1段階 第2段階
第2段階 第3段階
第3段階
 第2段階
第2段階
 第4段階
第4段階
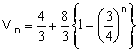 より,n→∞としたとき,Vn→12/3=4
より,n→∞としたとき,Vn→12/3=4
 頂点Nから,△KLMへ垂線を下ろした点をHとする。
頂点Nから,△KLMへ垂線を下ろした点をHとする。 より
より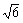
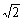

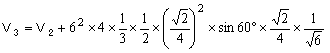
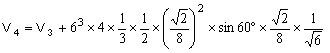
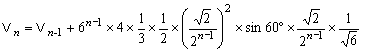
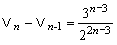 ∴
∴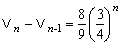 …①
…①