| (1) |
丂俹俠偺墑挿忋偵揰俢傪俹俛亖俠俢偲側傞傛偆偵偲傝丆恾偵婰擖偣傛丅乮free hand偱傛偄乯
|
 |
| (2) |
丂俙俹亖俙俢傪徹柧偣傛丅
|
|
| (3) |
丂俹俙亖俹俛亄俹俠傪徹柧偣傛丅
|
|
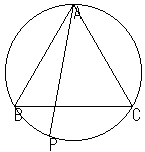
| (4) |
丂惓嶰妏宍俤俥俧偺奜晹偵揰俿傪壓恾偺傛偆偵偲傞丅仮俤俥俿傪俤傪拞怱偲偟偰惓偺曽岦偵60亱夞揮偝偣偨偲偒丆俿偺堏傞揰傪俽偲偡傞丅 丂俿俤亖俿俥亄俿俧側傜偽丆俿丆俧丆俽偼摨偠捈慄忋偵偁傞偙偲傪徹柧偣傛丅 |
 |
| 栤戣暥 |
丂惓嶰妏宍俙俛俠偵奜愙偡傞墌偺楎屖俛俠忋偺揰俹傪塃恾偺傛偆偵梌偊傞丅
| (1) |
丂俹俠偺墑挿忋偵揰俢傪俹俛亖俠俢偲側傞傛偆偵偲傝丆恾偵婰擖偣傛丅乮free hand偱傛偄乯
|
 |
| (2) |
丂俙俹亖俙俢傪徹柧偣傛丅
|
|
| (3) |
丂俹俙亖俹俛亄俹俠傪徹柧偣傛丅
|
|
| (4) |
丂惓嶰妏宍俤俥俧偺奜晹偵揰俿傪壓恾偺傛偆偵偲傞丅仮俤俥俿傪俤傪拞怱偲偟偰惓偺曽岦偵60亱夞揮偝偣偨偲偒丆俿偺堏傞揰傪俽偲偡傞丅 丂俿俤亖俿俥亄俿俧側傜偽丆俿丆俧丆俽偼摨偠捈慄忋偵偁傞偙偲傪徹柧偣傛丅 |
 |
| 拝娽揰 |
| 夝摎椺 |
| (1) | 徣棯乮恾偵婰擖乯 | 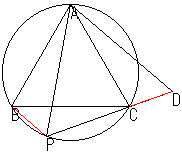 |
| (2) |
丂仮俙俛俹傪俙傪拞怱偲偟偰惓偺曽岦偵60亱夞揮偡傞偲俛偼俠偵堏傞丅 丂佢俙俠俢亖佢俙俛俹偐傜丆慄暘俛俹偼慄暘俠俢偵堏傞偐傜丆俹偼俢偵堏傞丅 丂偮傑傝偙偺夞揮偵傛偭偰仮俙俛俹偼仮俙俠俢偵堏傞丅 丂丂丂亪仮俙俛俹佭仮俙俠俢丂丂亪俙俹亖俙俢 亙暿徹亜 丂巐妏宍俙俛俹俠偼墌偵撪愙偡傞偐傜 丂丂丂佢俙俠俢亖佢俙俛俹丂偐偮丂俙俠亖俙俛丆俠俢亖俹俛 丂傛偭偰丆2曈偲偦偺偼偝傓妏偑摍偟偄偐傜 丂丂丂仮俙俛俹佭仮俙俠俢丂丂亪俙俹亖俙俢 |
|
| (3) |
丂俙俢偼俙俹傪60亱夞揮偟偨傕偺偱偁傞偐傜丆仮俙俹俢偼惓嶰妏宍偱偁傞丅 丂丂丂亪俹俢亖俹俙 丂丂丂亪俹俙亖俹俢亖俹俠亄俠俢亖俹俛亄俹俠 亙暿徹亜 丂(2)傛傝丆俙俢亖俙俹丂乧乧嘆 丂傑偨丆佢俢俙俠亖佢俹俙俛 丂丂丂亪佢俢俙俹亖60亱丂乧乧嘇 嘆嘇傛傝仮俙俹俢偼惓嶰妏宍偱偁傞丅 丂丂丂亪俹俢亖俹俙 丂丂丂亪俹俙亖俹俢亖俹俠亄俠俢亖俹俛亄俹俠 |
|
| (4) |
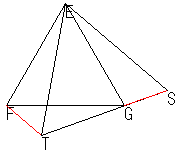 仮俤俥俿傪俤傪拞怱偲偟偰惓偺曽岦偵60亱夞揮偟偨偲偒丆俿偺堏傞揰偑俽偩偐傜丆
仮俤俥俿傪俤傪拞怱偲偟偰惓偺曽岦偵60亱夞揮偟偨偲偒丆俿偺堏傞揰偑俽偩偐傜丆丂丂丂仮俤俥俿佭仮俤俧俽丂丂亪俿俥亖俧俽丂乧乧嘊 丂傑偨丆 丂丂丂俿俤亖俽俤丂偐偮丂佢俽俤俿亖佢俧俤俥亖60亱 備偊偵丆仮俤俿俽偼惓嶰妏宍偱偁傞丅 丂丂丂亪俿俤亖俿俽 丂壖掕傛傝丆俿俤亖俿俥亄俿俧丂偩偐傜 丂丂丂俿俽亖俿俧亄俧俽丂乮佹嘊乯 傛偭偰丆俿丆俧丆俽偼摨偠捈慄忋偵偁傞丅乮徹柧廔乯 |
|