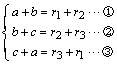
だから(①+②+③)/2 より a+b+c=r1+r2+r3 …④
④-②、④-③、④-① から a=r1,b=r2,c=r3
A,B,CはそれぞれP,Q,Rと一致する。すなわち、内接円は3点P,Q,Rを通る。
(2)余弦定理より、
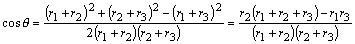
(3)正弦定理より、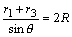 よって、
よって、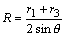 …①
…①
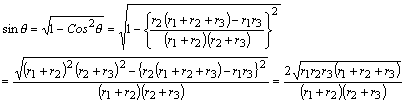
故に、①に代入して、 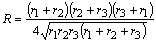
北海道札幌新川高校 教諭 佐々木光憲
| 着眼点 |
| 解答例 |
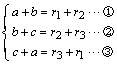
(2)余弦定理より、
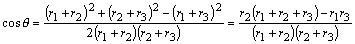
(3)正弦定理より、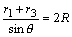 よって、
よって、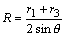 …①
…①
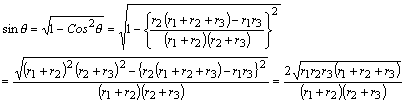
故に、①に代入して、 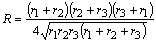
北海道札幌新川高校 教諭 佐々木光憲