| 着眼点 |
| 解答例 |

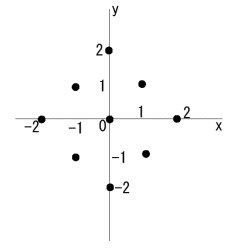
| 点(0,0) | 確率 1/4 |
| 点(1,1) | 確率 1/8 |
| 点(1,−1) | 確率 1/8 |
| 点(−1,1) | 確率 1/8 |
| 点(−1,−1) | 確率 1/8 |
| 点(2,0) | 確率 1/16 |
| 点(−2,0) | 確率 1/16 |
| 点(0,2) | 確率 1/16 |
| 点(0,−2) | 確率 1/16 |
(2) y=x+k (−3≦k≦3) 上の点として、3秒後に移動可能な点は、k=±3±1 のときで、
k=3のとき、
(−3,0),(−2,1),(−1,2),(0,3) の4点。
それぞれ道の数は、1,3,3,1通りあるので、求める確率は、
(1+3+3+1)/43=1/8
K=−3のときも、上と原点対称なので、確率 1/8
K=1のとき、
(−2,−1),(−1,0),(0,1),(1,2) の4点。
それぞれ道の数は3,9,9,3通りあるので、求める確率は、
(3+9+9+3)/43=3/8
K=−1のときも、上と原点対称なので、確率 3/8
K=±3のとき、確率 1/8,K=±1のとき、確率3/8,K=0±2のとき 確率0
(3)y=x+k (−n≦k≦n)上の点として、n秒後に移動可能な点は
k=±n,±(n−2),±(n−4),…
k=nのとき、
(−n,0),(−n+1,1),…,(0,n) の(n+1)点
それぞれの道の数は、
(nC0+nC1+…+nCn)/4n=2n/4n=1/2n
k=n−2のとき
(−n+1,−1),(−n+2,0),…,(1,n−1) の(n+1)点
それぞれの道の数は、nC1×nC0,nC1×nC1,…,nC1×nCn 通あるので、
求める確率は、nC1×(nC0+nC1+…+nCn)/4n=nC1×2n/4n=nC1/2n
一般に、k=n−2r (0≦r≦n) のとき、直線 y=x+k上の点
(−n+r+l,−r+l) (0≦l≦n) に行く道の数は、nCr×nCl であることを示しておく。
→がa個、←がb個、↑がc個、↓がd個(a+b+c+d=n)の順列の中で
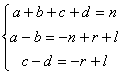
を満たすもの数を求めることになる。
上の連立方程式から、a+c=l,b+d=n−l だから、(a+c)個の→と↑の入れ場所の選び方は、nCl 通りある。残りが(b+d)個の←と↓の入る場所である。
また、a+d=r,b+c=n−r なので、nCl 通りの場所選びの各々に対して、(a+d)個の→と↓の場所選びは、nCr 通りずつあるので、求める順列の総数は、
nCr×nCl
となる。
故に、k=n−2r (0≦r≦n) のとき、求める確率は
nCr/2n