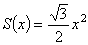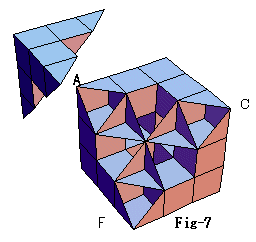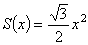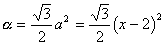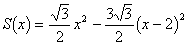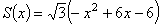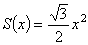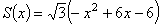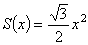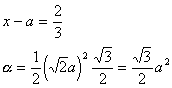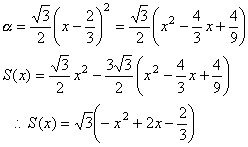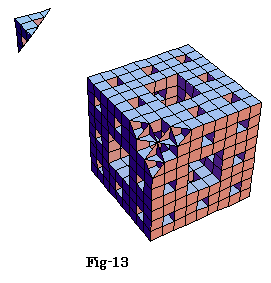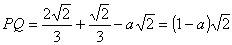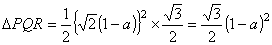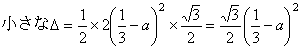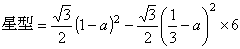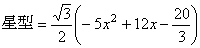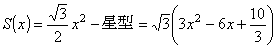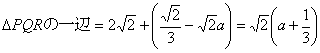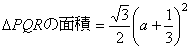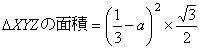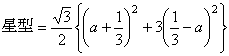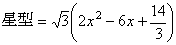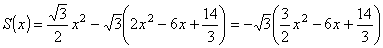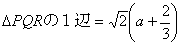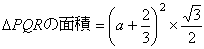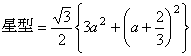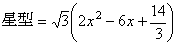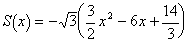【TOP】
【解答4】
解 答 5
フラクタル的3次元立体図形を、いくつかの2次元的平面図形の情報を用いて、断片的に把握し、
立体全体を理解する問題です。
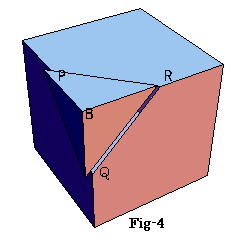 問1
問1
PB=QB=RB=x とおくと△PBRは直角二等辺三角形より
PR=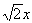
断面積PQRは1辺が、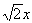 の正三角形である。
の正三角形である。
断面積をS(x)とおくと
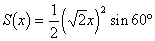
∴ 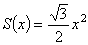 …(答)
…(答)
 問2
問2
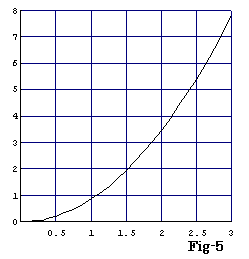
∴ 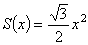
グラフはFig-5の様になる。
問3
切断するとFig-6が切断面、Fig-7が切断した立体。
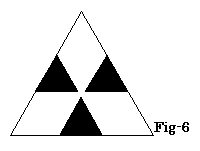
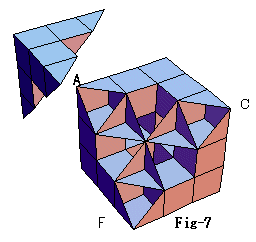
問4
- 0≦x≦2の時
∴ 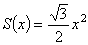
- 2≦x≦3の時
x−a=2とおく
中央の切除部分による断面積の欠落面積をαとおく。
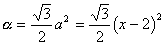
断面積をS(x)とおくと
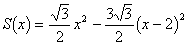
展開すると
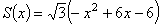
まとめると
- 0≦x≦2の時
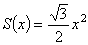
- 2≦x≦3の時
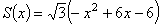
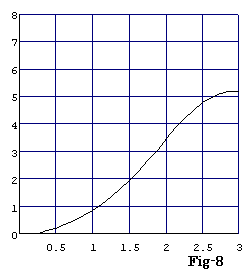
これらをグラフにすると、Fig-8になる。
問5

- 0≦x≦2/3の時
断面積をS(x)とおく
∴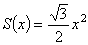
- 2/3≦x≦1の時
中央の切除部分による断面積の欠落面積をαとおく。
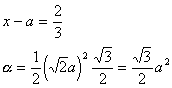
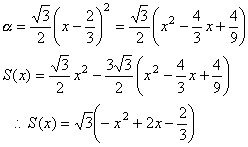
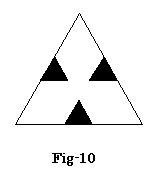
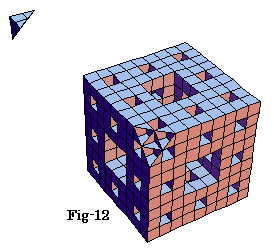
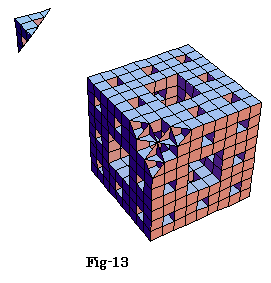
- 1≦x≦4/3の時
α=x−1とおく
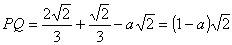
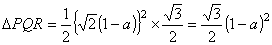
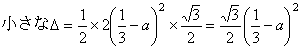
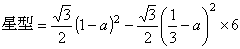
α=x-1を代入
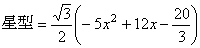
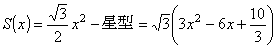
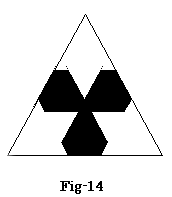
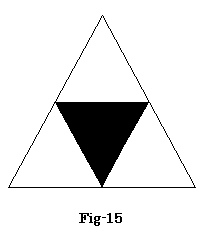

- 4/3≦x≦5/3の時
α=x−4/3とおく
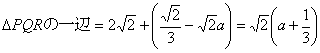
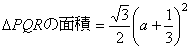
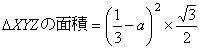
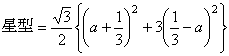
α=x−4/3を代入すると
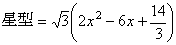
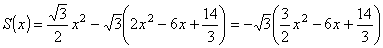

- 5/3≦x≦2の時
α=x−5/3とおく
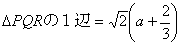
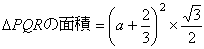

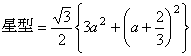
α=x−5/3を代入すると
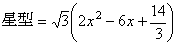
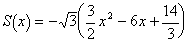

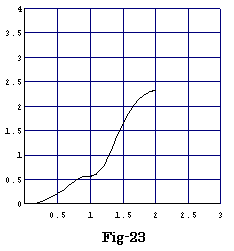
以上のS(x)の変化をグラフにするとFig-23になる。
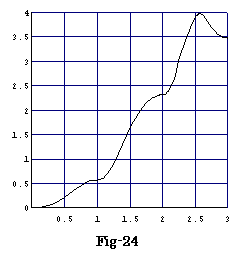
この問5は0≦x≦2の変化であるが、更に0≦x≦3まで変化させると、Fig-24のグラフになる。この時、断面積が減少するケ−スも見られ、非常に興味深い変化が見られる。はたして、この断面積の変化のグラフもフラクタル的になっているのだろうか?
問題5について
この問題5を作成するにあたって、
- 理論的・抽象的である数学を目に見える模型やコンピュ−タ―・グラフィックスで表現して、見て考える事ができる問題。
- 考える過程において、数学的美しさと感動を感じる事のできる問題。
をテ−マにした。
1998年旭川市で実施された、
数学にさわろう『Mathematical Art展』数理と造形の融合
〔委員長 西山恒夫先生・副委員長 大矢二郎先生 秋山仁先生〕
において、出展された、
「穴開き立方体を切ってビックリ―三菱マ−クが現れる立体―」
(東海大学教育開発研究所 岩間大介先生作成)
をヒントに作成した。
更に、CGに関しては、滋賀県河瀬高校 高橋英和先生が考案した、Mathematica3.0で作動するknifeというパッケ−ジを利用させていただき、いろいろな3次元フラクタル図形を切断し、その切断面の形状や面積の変化について考える問題を作成しました。
採点基準は
(1)PR=√2xまで4点 小計8点
(2)4点
(3)8点
(4)0≦x≦2の場合3点 2≦x≦3の場合3点 グラフ2点 小計8点
(5)0≦x≦2/3の場合1点、2/3≦x≦1の場合2点、
1≦x≦4/3の場合2点、4/3≦x≦5/3の場合2点、5/3≦x≦2の場合2点、
グラフ3点 小計12点
合計40点
採点して気がついたこととして
(3)は数式を使わなくても「空間図形的な想像力」を利用して考える事を期待して出題した。(3)のみを解答している生徒も多く、予想もしない珍解答も見られた。
(5)はかなり複雑な形状の変化を解析しなければならないので、完璧に解答する生徒は見られなかったが、札幌北高校2年佐藤俊介君、北嶺中学3年高橋健君、札幌南高校1年中村静香さん、2年榎戸輝揚君、2年伊藤亮孝君、札幌東高校1年穴澤裕一君、2年篠崎隆章君、小樽潮陵高校1年箕輪寛君、滝川高校2年宇戸勇太君らは鋭く3次元フラクタル図形を分析して「論理に組み立て」「数式の変形」もきちんとされた説得力ある立派な解答でした。
イギリスのHounsfieldにより発明された「CTスキャン」(Computed Tomography)は、近年の画像診断上欠かせない、重要な分野になっているが、人体のような3次元フラクタル図形を、多くの輪切り状態の画像を作成し、これらの情報を統合して、複雑な立体の構造を解析しようとする方法の簡単な例だと認識して下さい。
今回の数学コンテストに参加された北海道の高校生の皆さん、例え誤答であっても、自分で考える事、そして挑戦することが重要であると思います。
「試される大地 北海道 一歩前に出る勇気があれば、きっと何かが始まる。」の精神で、日々の高校生活をそして、来年の21世紀の数学コンテストにも挑戦して欲しいと思います。
北海道札幌平岡高等学校 教諭 松本睦郎
【TOP】
【解答4】
 問1
問1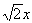
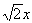 の正三角形である。
の正三角形である。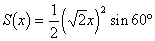
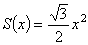 …(答)
…(答)
 問2
問2