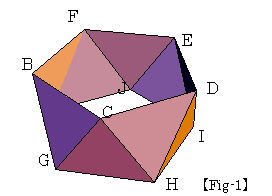【TOP】【解答】
第19回
北海道高等学校数学コンテスト
問 題
平成13年1月12日(金)
9時00分〜12時30分(210分)実施問題1
1とその数自身の2つの数によってしか割り切れない数を素数という。
次の表は「エラトステネスのふるい」と呼ばれるものである。この表を参考に以下の問いに答えなさい。エラトステネスのふるい自然数の表を作り、2の倍数、3の倍数、5の倍数と、
素数の倍数を順に消していけば、後に素数だけが残る。

(1) 1次関数 f(x)=ax+b(a,b は整数)で、f(0),f(1),f(2) の値が異なる3つの素数となるようなf(x) を一つ求めよ。
(2) 2次関数 f(x)=ax2+bx+c( a,b,cは整数)で f(0),f(1),f(2) の値が異なる3つの素数となるような f(x) を一つ求めよ。
(3) 2次関数 f(x)=ax2+bx+c( a,b,cは整数)でf(0),f(1),f(2),f(3) の値が異なる4つの素数となるようなf(x) を一つ求めよ。また、そのとき f(5) も素数となるか調べよ。
問題2
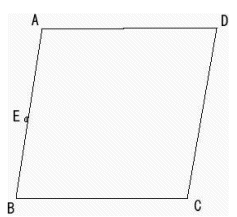
下図のようにひし形ABCDEの辺AB上に1点Eが存在している。(1) CEとBDの交点をFとするとき、3点A,E,Fを通る円を作図せよ。
(2) 3点A,E,Fを通る円が再び直線AD,BDと交わる点をそれぞれP,Qとするとき4点B,C,Q,Eは同一円周上にあることを証明せよ。
(3) 4点C,F,P,Dは同一円周上にあることを証明せよ。
(4) 3点C,Q,Pは一直線にあることを証明せよ。
問題3
xの2次方程式 x2−2ax+1=0 の2つの解を α,β (α<β)とするとき、次の問いに答えなさい。ただし、αは2以上の整数とする。(1) α,βを求め、αβ の値も求めなさい。
(2) α2+β2 は偶数であることを示しなさい。ただしnは自然数とする。
(3) βn の整数部分をm、小数部分をs (0<s<1) とするとき、mは奇数であることを示しなさい。
(4) mをsを用いて表しなさい。
問題4
整数 a,b の最大公約数が1であるとき、a,b は互いに素であるという。いま、自然数nに対して、1からnまでの数字を一つずつ書いたn枚のカードから1枚を取り出すとき、それがnと互いに素な数字のカ−ドである確率をf(n) で表すことにする。このとき次の問いに答えよ。(1) f(8),f(108),f(2001) の値を求めよ。
(2) n=pk (pは素数、k≧1) のとき、f(n) を求めなさい。
(3) n=pk×ql (p,q は異なる素数、k,l≧1 )のとき、f(n) を求めなさい。
問題5
1辺の長さが1の正三角形を10個つなげた展開図を組みたてて右下図Fig-1の様な立体を作成した。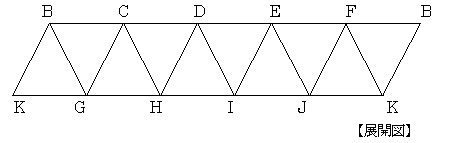
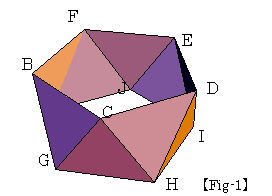
ただし、上面のBCDEFと底面KGHIJは正五角形であるものとする。
(1) 上面の正五角形BCDEFにおいて、線分CFの長さを求めよ。
(2) 線分FHの長さを求めよ。
(3) 正五角形BCDEFを上面、正五角形KGHIJを底面とするとき、この立体の高さを求めよ。
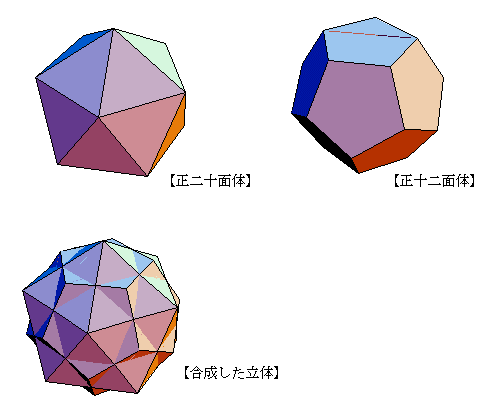
(4) 1辺の長さが1の正二十面体と1辺の長さがaの正十二面体を下図のように、お互いの各辺が垂直二等分する様に合成した立体について考える。このとき、aの値を求めよ。
【TOP】-->【概評】【解答】