∴ｆ(ｘ)＝２ｘ＋３
（２）２次関数となるためには、ｙの増加率が異なっている３点を選べばよいのだから、これは易しい。但し、係数が整数であることに注意。増加率が２，４などと変化していくところに注意して、係数が整数であるから１１，１３，１７ととってみる。
ｆ(ｘ)＝ａｘ2＋ｂｘ＋ｃとおいてｃ＝１１，ａ＋ｂ＋１１＝１３，４ａ＋２ｂ＋１１＝１７から、ａ＝ｂ＝１，ｃ＝１１がでる。
∴ｆ(ｘ)＝ｘ2＋ｘ＋１１ 他にも１７，１９，２３をｙの値としてとる。ｆ(ｘ)＝ｘ2＋ｘ＋１７ などがある。
他にも、いろいろ求められる、いずれも正解である。
（３）２が偶数なので (２，３，５，７) はありえない。３，５，７ のところの増加率も一定の２．(１１，１３，１７，１９)は、増加率が２，４，２となっているで、ありえない。こんな風に見ていくと、妥当なところは増加率が２，４，６となっている(４１，４３，４７，５３)だろうと見当がつくはずである。２年生では、ｙ＝ｘ2 を微分すると ｙ'＝２ｘ 、更に微分して ｙ''＝２ となることを思い出して欲しい。
ｆ(ｘ)＝ａｘ2＋ｂｘ＋ｃ とおいて、ｆ(０)＝４１，ｆ(１)＝４３，ｆ(２)＝４７，ｆ(３)＝５３ から
ｃ＝４１，ａ＋ｂ＝２，２ａ＋ｂ＝３
がでる。これを解いて、 ａ＝ｂ＝１，ｃ＝４１
∴ｆ(ｘ)＝ｘ2＋ｘ＋４１
ｆ(３)＝９＋３＋４１＝５３ 題意は満たされている。ｆ(５) はどうだろうか？
ｆ(５)＝２５＋５＋４１＝７１ これも素数である。
次の文章は、「フェルマ−の最終定理に挑戦」（富永裕久著、ナツメ社）からの抜粋です。是非一読をお薦めします。
素数が無限に存在することや素数の分布など、素数についてはさまざまなことが古代から研究されている。しかし必ず素数を生み出す公式は、まだ発見されていない。 すべての素数をつくり、しかも素数以外はつくらない公式はもちろんのこと、モレはあっても素数の みを生み出す公式も見つかっていないのだ。
素数のみを生み出す公式として予想されたのがフェルマ−数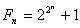 
であったが、ｎ＝５ であっけなく破綻してしまった。この間違いを発見したのはオイラ―だが、オイラ−自身、素数をかなりの確率で生み出す公式を発見している。
Ｐ＝ｎ2＋ｎ＋４１ である。ｎに０から順に整数を代入してみればわかるが、
４１，４３，４７，５３，６１，７１，８３，９７，１１３，１３１，１５１，１７３・・・
と素数がしばらくはどこまでも続く。ただし、それもｎ＝３９の１６０１まで。次のｎ＝４０では１６８１(＝４１2)となってしまう。しかし１０００万以下の素数のうち４７．５％の素数を突き止めるという驚異的な式である。
このほかに ４ｎ2＋１７０ｎ＋１８４７や ４ｎ2＋４ｎ＋５９などが、かなりの確率で素数を生み出す式として知られている。
しかし、冒頭で述べたように、素数のみを生み出す公式。そして、すべての素数をもれなくつくり、しかも素数以外はつくらない公式があるかどうかは謎である。