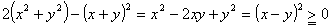
丂丂傛偭偰丄
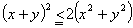 丂摍崋偼倶亖倷偺偲偒
丂摍崋偼倶亖倷偺偲偒
乮俀乯晄摍幃傪倶偵偮偄偰惍棟偡傞偲
丂丂丂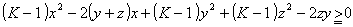
丂俲亝侾側傜嵍曈亙侽偲側傞応崌偑弌偰偔傞偺偱俲亜侾
丂倶偺俀師曽掱幃偲傒偨偲偒丄敾暿幃傪俢1偲偍偔偲
丂丂丂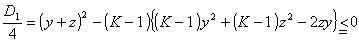
丂倷偵偮偄偰惍棟偡傞偲
丂丂丂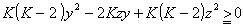
丂侾亙俲亝俀側傜嵍曈亙侽偲側傞応崌偑弌偰偔傞偺偱丄俲亜俀
丂倷偺俀師曽掱幃偲傒偨偲偒丄敾暿幃傪俢2偲偍偔偲
丂丂丂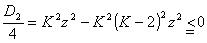
丂丂丂(俲亅俁)(俲亅侾)亞侽丂丂丂俲亜俀側偺偱丄俲亞俁
丂傛偭偰丄惓偺掕悢俲偺嵟彫抣偼俁偱偁傞丅乮摍崋惉棫偼倶亖倷亖倸偺偲偒乯
亂乮俀乯偺暿夝亃倶2亄倷2亄倸2亜侽偺偲偒
丂丂丂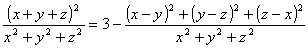
丂傛傝嵟彫抣俁乮摍崋惉棫偼倶亖倷亖倸偺偲偒乯
丂乮俁乯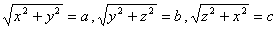 偲偍偔偲
偲偍偔偲
丂丂丂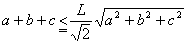
丂乮俀乯偺寢壥傛傝俴偺嵟彫抣偼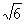 偲側傞丅摍崋惉棫偼|倶|亖|倷|亖|倸|偺偲偒
偲側傞丅摍崋惉棫偼|倶|亖|倷|亖|倸|偺偲偒
丂乮係乯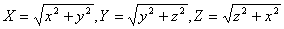 偲偍偔偲倃亞侽丆倄亞侽丆倅亞侽偱偁傝丄
偲偍偔偲倃亞侽丆倄亞侽丆倅亞侽偱偁傝丄
丂丂丂倃2亄倄2亞倅2丆倄2亄倅2亞倃2丆倅2亄倃2亞倄2
丂倃亖倄亖倅亖侽偡側傢偪倶亖倷亖倸亖侽偺偲偒偼丄俵偼擟堄偺惓偺悢偱惉棫丅
丂倃2亄倄2亞倅2偺偲偒
丂(鶣)倅亖侽側傜丄倸亖倶亖侽偲側傝丄倃亖倄亖|倷|亜侽偩偐傜
丂丂丂 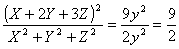
丂(鶤)倅亜侽側傜丄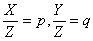 偲偍偔偲丄
偲偍偔偲丄
丂丂丂忦審倃2亄倄2亞倅2丆倄2亄倅2亞倃2丆倅2亄倃2亞倄2偼倫2亄倯2亞侾丆倯2亄侾亞倫2丆侾亄倫2亞倯2乮倫,倯亞侽乯
丂丂丂丂 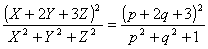
丂偄傑丄倫2亄倯2亖倰2乮倰亞侾乯偲偍偔偲丄(倫亄倯)2亄(俀倫亅倯)2亖俆(倫2亄倯2) 偐傜丄
丂丂丂丂 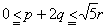 乮摍崋偼丄俀倫亖倯 乯
乮摍崋偼丄俀倫亖倯 乯
丂傛偭偰
丂丂丂丂 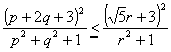 丂乮摍崋偼丄俀倫亖倯 乯
丂乮摍崋偼丄俀倫亖倯 乯
丂丂丂丂 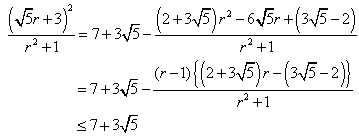 丂乮摍崋偼倰亖侾 乯
丂乮摍崋偼倰亖侾 乯
丂摍崋惉棫偼丄倰亖侾偐偮俀倫亖倯傛傝丄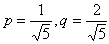 偺偲偒丆偡側傢偪
偺偲偒丆偡側傢偪
丂丂丂丂 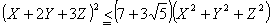
丂偱摍崋惉棫偼丄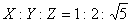 偺偲偒
偺偲偒
丂丂丂丂 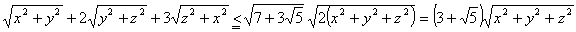
丂偑惉傝棫偪丄摍崋惉棫偼丄(倶2亄倷2)丗(倷2亄倸2)丗(倸2亄倶2)亖侾丗係丗俆偺偲偒偱
丂偡側傢偪丄倷亖侽丆|倶|丗|倸|亖侾丗俀
丂屘偵丄俵偺嵟彫抣偼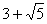 偱丄摍崋偑惉傝棫偮偺偼倷亖侽丆|倶|丗|倸|亖侾丗俀偺偲偒偱偁傞丅
偱丄摍崋偑惉傝棫偮偺偼倷亖侽丆|倶|丗|倸|亖侾丗俀偺偲偒偱偁傞丅