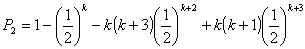(ⅰ)Bが1勝すると優勝、ゆえにBが優勝する確率は
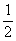
よって、
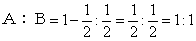
(ⅱ)Bが2勝すると優勝、ゆえにBが優勝する確率は
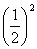
よって、
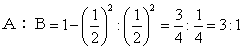
(ⅲ)Bが3勝すると優勝、ゆえにBが優勝する確率は
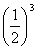
よって、
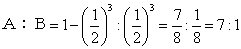
(ⅳ)Bが4勝すると優勝、ゆえにBが優勝する確率は
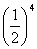
よって、
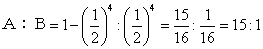
(ⅴ)Bが5勝すると優勝、ゆえにBが優勝する確率は
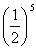
よって、
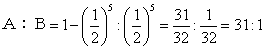
(2)Bがk勝すると優勝 ゆえにBが優勝する確率は
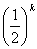
よって、
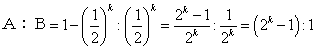
(3)Bが優勝するのは、次の2つの場合である。
(ア)Bがk勝する場合
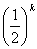
(イ)Aが1勝、Bがk-1勝した後、次のゲ-ムでBが勝つ場合
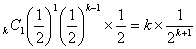
(ア)+(イ)よりBが優勝する確率は、
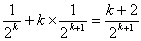
よって、
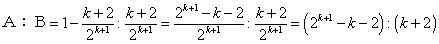
(4)Bが優勝するのは、次の3つの場合がある。
(ア)Bがk勝する場合
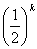
(イ)Aが1勝、Bがk-1勝した後、次のゲ-ムでBが勝つ場合
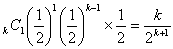
(ウ)Aが2勝、Bがk-1勝した後、次のゲ-ムでBが勝つ場合
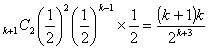
(ア)+(イ)+(ウ)よりBが優勝する確率は、
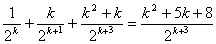
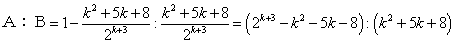
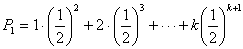 …①
…①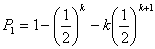
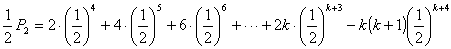 …③
…③