(2)8通り
(3)格子点には型があり、下記のようにⅠ型(左図)、Ⅱ型(右図)とする。
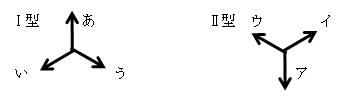
Ⅰ型から出発すれば、全てⅡ型に入り、Ⅱ型から出発すれば、全てⅠ型にはいる。
だから、最短経路の文字を並べれば、「カタカナ」と「ひらがな」が互いに入れ替わりながら並ぶことになる。また、「あ」と「ア」、「い」と「イ」、「う」と「ウ」は互いに逆方向とする。
そこで、ある格子点Eから、別の格子点Fへ行く最短経路が偶数の場合で考える。
EからFへ行く最短経路の中には「あ」と「ア」、「い」と「イ」、「う」と「ウ」は同時に存在しない。なぜなら、もし、同時に存在した場合、互いに逆方向に進む辺が存在するので、お互いに方向を打ち消しあうことになる。さらに、短い経路が存在する。
よって、存在する文字の種類は多くても3文字である。1文字は存在しない。よって、存在するパターンは、2文字または3文字になる。
すると、最短経路の辺の組み合わせパターンは、3種類の方向が存在する場合(あ、い、ウ)、(あ、イ、う)、(ア、い、う)、(あ、イ、ウ)、(ア、い、ウ)、(ア、イ、う)の6パターンであり、2種類のみの方向が存在する場合(あ、イ)、(ア、い)、(あ、ウ)、(ア、う)、(い、ウ)、(イ、う)の6パターンである。
いずれのパターンでも、その中には、1文字しか存在しない「カタカナ」または、「ひらがな」がある。そして、「カタカナ」と「ひらがな」が交互に並んでいるので、その1文字しかない「カタカナ」または「ひらがな」が、全部の辺の数の半分だけ存在することになる。よって、最短経路の辺の数の半分は、同一方向に進む辺になる。
(例)あ、イ、あ、ウ、あ、ウ、あ、イ、あ、ウ、→「あ」が5回、「イ」が2回、「ウ」が3回である。
(4)
(ⅰ)使用される文字が2種類の場合
「カタカナ」1文字と「ひらがな」1文字である。1通り存在する。
(ⅱ)使用される文字が3種類の場合
1文字しか存在しない「カタカナ」または「ひらがな」はN個ある。
残りのN個の中の少ない方の辺の数をkとする。(k≦N)
k個と(N-k)個の2種類の文字の配列の個数が求める経路の通りになるので、NCKとなる。