乮侾乯晄摍幃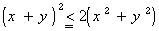 傪徹柧偣傛丅傑偨丄摍崋偑惉傝棫偮偺偼偳傫側偲偒偐摎偊傛丅
傪徹柧偣傛丅傑偨丄摍崋偑惉傝棫偮偺偼偳傫側偲偒偐摎偊傛丅
乮俀乯晄摍幃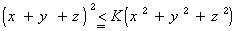 傪枮偨偡嵟彫側惓偺掕悢俲偑俁偱偁傞偙偲傪徹柧偣傛丅傑偨丄摍崋偑惉傝棫偮偺偼偳傫側偲偒偐摎偊傛丅
傪枮偨偡嵟彫側惓偺掕悢俲偑俁偱偁傞偙偲傪徹柧偣傛丅傑偨丄摍崋偑惉傝棫偮偺偼偳傫側偲偒偐摎偊傛丅
乮俁乯晄摍幃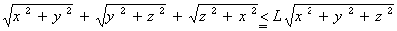 傪枮偨偡惓偺掕悢俴偺嵟彫抣傪媮傔傛丅傑偨丄摍崋偑惉傝棫偮偺偼偳傫側偲偒偐摎偊傛丅
傪枮偨偡惓偺掕悢俴偺嵟彫抣傪媮傔傛丅傑偨丄摍崋偑惉傝棫偮偺偼偳傫側偲偒偐摎偊傛丅
乮係乯晄摍幃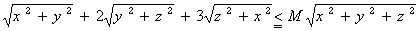 傪枮偨偡惓偺掕悢俵偺嵟彫抣傪媮傔傛丅傑偨丄摍崋偑惉傝棫偮偺偼偳傫側偲偒偐摎偊傛丅
傪枮偨偡惓偺掕悢俵偺嵟彫抣傪媮傔傛丅傑偨丄摍崋偑惉傝棫偮偺偼偳傫側偲偒偐摎偊傛丅
栤戣侾
乮侾乯晄摍幃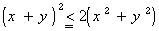 傪徹柧偣傛丅傑偨丄摍崋偑惉傝棫偮偺偼偳傫側偲偒偐摎偊傛丅
傪徹柧偣傛丅傑偨丄摍崋偑惉傝棫偮偺偼偳傫側偲偒偐摎偊傛丅
乮俀乯晄摍幃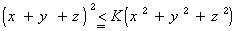 傪枮偨偡嵟彫側惓偺掕悢俲偑俁偱偁傞偙偲傪徹柧偣傛丅傑偨丄摍崋偑惉傝棫偮偺偼偳傫側偲偒偐摎偊傛丅
傪枮偨偡嵟彫側惓偺掕悢俲偑俁偱偁傞偙偲傪徹柧偣傛丅傑偨丄摍崋偑惉傝棫偮偺偼偳傫側偲偒偐摎偊傛丅
乮俁乯晄摍幃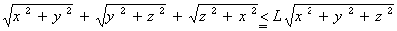 傪枮偨偡惓偺掕悢俴偺嵟彫抣傪媮傔傛丅傑偨丄摍崋偑惉傝棫偮偺偼偳傫側偲偒偐摎偊傛丅
傪枮偨偡惓偺掕悢俴偺嵟彫抣傪媮傔傛丅傑偨丄摍崋偑惉傝棫偮偺偼偳傫側偲偒偐摎偊傛丅
乮係乯晄摍幃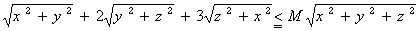 傪枮偨偡惓偺掕悢俵偺嵟彫抣傪媮傔傛丅傑偨丄摍崋偑惉傝棫偮偺偼偳傫側偲偒偐摎偊傛丅
傪枮偨偡惓偺掕悢俵偺嵟彫抣傪媮傔傛丅傑偨丄摍崋偑惉傝棫偮偺偼偳傫側偲偒偐摎偊傛丅
栤戣俀
乮侾)値亖俆偺偲偒丄師偺奺応崌偵偮偄偰摎偊側偝偄丅
丂(鶣)丂俙偑4彑丄俛偑4彑偱拞抐偟偨応崌丏
丂(鶤)丂俙偑4彑丄俛偑3彑偱拞抐偟偨応崌丏
丂(鶥)丂俙偑4彑丄俛偑2彑偱拞抐偟偨応崌丏
丂(鶦)丂俙偑4彑丄俛偑1彑偱拞抐偟偨応崌丏
丂(鶧)丂俙偑4彑丄俛偑0彑偱拞抐偟偨応崌丏
乮俀乯値偑値亞侾偺帺慠悢偺偲偒丄俙偑値亅侾彑丄俛偑値亅倠彑乮侾亝倠亝値丆倠偼帺慠悢乯偱拞抐偟偨応崌丅
乮俁乯値偑値亞俀偺帺慠悢偺偲偒丄俙偑値亅2彑丄俛偑値亅倠彑乮俀亝倠亝値丆倠偼帺慠悢乯偱拞抐偟偨応崌丅
乮俆乯値偑値亞俁偺帺慠悢偺偲偒丄俙偑値亅3彑丄俛偑値亅倠彑乮俁亝倠亝値丆倠偼帺慠悢乯偱拞抐偟偨応崌丅
栤戣俁
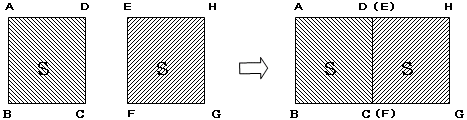
 傪庢傝彍偒丄巆偭偨暵嬫娫
傪庢傝彍偒丄巆偭偨暵嬫娫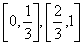 偺偦傟偧傟傪傑偨3摍暘偟偰拞墰偺奐嬫娫傪庢傝彍偔丄偙偺憖嶌傪師乆孞傝曉偡傕偺偲偡傞丅
偺偦傟偧傟傪傑偨3摍暘偟偰拞墰偺奐嬫娫傪庢傝彍偔丄偙偺憖嶌傪師乆孞傝曉偡傕偺偲偡傞丅
乮侾乯俧2傪媮傔側偝偄丅傑偨丄偙傟傜偺暵嬫娫偺挿偝偺憤榓傪媮傔側偝偄丅
乮俀乯俧n偵擖偭偰偄傞暵嬫娫偺屄悢傪媮傔側偝偄丅傑偨丄偙傟傜偺暵嬫娫偺挿偝偺憤榓傪媮傔側偝偄丅
乮俁乯俧5偵擖偭偰偄傞暵嬫娫偱丄16斣栚偺傕偺傪媮傔側偝偄丅偨偩偟丄暵嬫娫偺弴斣偼丄椉抂偺悢偑彫偝側傞傕偺偐傜弴斣晅偗傞傕偺偲偡傞丅
乮係乯俧n偵擖偭偰偄傞暵嬫娫偱丄俀n-1亅俁斣栚偺傕偺傪媮傔側偝偄丅偨偩偟丄暵嬫娫偺弴斣偼丄椉抂偺悢偑彫偝側傞傕偺偐傜弴斣晅偗傞傕偺偲偡傞丅
栤戣係
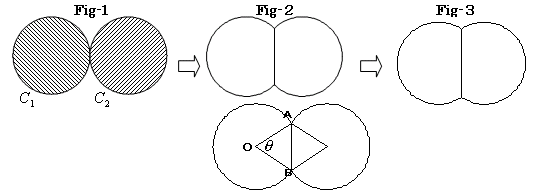
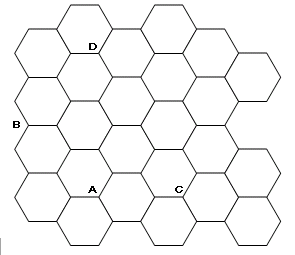
乮侾乯恾偺拞偵奿巕揰俙丆俛傪庢傝丄俙仺俛傊峴偔嵟抁宱楬偺曈偺悢傪媮傔傛丅
乮俀乯乮侾乯偲摨條偵偟偰丄恾拞偺俠仺俢傊峴偔嵟抁宱楬偺曈偺悢傪媮傔傛丅
乮俁乯偄傑丄嵟抁宱楬偺悢偑嬼悢偱偁傞帪丄偦偺敿暘偺悢偩偗偼丄摨堦曽岦偵恑傓曈偵側傞偙偲傪帵偣丅
乮係乯乮俁乯偺応崌丄嵟抁宱楬偼壗捠傝偁傞偐丅乮曈偺悢傪俀俶偲偡傞丅傑偨懠偵昁梫偑偁傟偽丄揔媂丄暥帤傪愝掕偟偰椙偄丅乯
栤戣俆
乮侾乯墌傪丄惓曽宍丄捈妏擇摍曈嶰妏宍丄惓榋妏宍偵曄宍偟偨帪丄偦傟偧傟偺廃埻偺挿偝偺戝彫傪斾妑偟戝彫弴偵暲傃曄偊傛丅