

 ソースファイル 1
ソースファイル 1
|
ここをクリックするとサンプルファイルのダウンロードができます。 (sample.LZH 5kb) |
アポロニュース2.BAS

SET WINDOW 0,1,0,1
SET POINT STYLE 3
GET POINT: x1,y1
PLOT POINTS:x1,y1
GET POINT: x2,y2
PLOT POINTS:x2,y2
SET LINE COLOR 4
PLOT LINES:X1,Y1;X2,Y2
DO
mouse poll x3,y3,L,R
if L=1 then
set point color 0
plot points: p,q
set line color 0
plot lines:x1,y1;p,q;x2,y2
set point color 3
SET POINT STYLE 4
plot points: x3,y3
set LINE color 7
plot LINEs:X1,Y1;X3,Y3;X2,Y2
let p=x3
let q=y3
end if
loop until R=1
LET m=SQR((X1-X3)^2+(Y1-Y3)^2)
LET n=SQR((X2-X3)^2+(Y2-Y3)^2)
let x4=(n*x1+m*x2)/(m+n)
let y4=(n*y1+m*y2)/(m+n)
let x5=(-n*x1+m*x2)/(m-n)
let y5=(-n*y1+m*y2)/(m-n)
let a=(x4+x5)/2
let b=(y4+y5)/2
set point color 2
plot points:a,b
let r=sqr((x4-a)^2+(y4-b)^2)
FOR t=0 TO 2*pi STEP pi/45
PLOT points:a+r*cos(t),b+r*sin(t)
plot lines:x1,y1;a+r*cos(t),b+r*sin(t);x2,y2
for s=0 to 100 step 0.02
next s
NEXT t
set line color 4
plot lines:x1,y1;x2,y2
END
お絵描き.BAS
set window -10,10,-10,10
INPUT PROMPT "a,b=":a,b
draw grid
set point style 4
do
mouse poll x,y,L,R
if L=1 then
set point color 3
let t=angle(a,b)
let r=sqr(a^2+b^2)
plot points: x,y
set point color 4
plot points:r*(x*cos(t)-y*sin(t)),r*(x*sin(t)+y*cos(t))
else
plot lines
end if
loop until R=1
end
お絵描き2.BAS
set window -10,10,-10,10
draw grid
input prompt "p,q=":p,q
INPUT PROMPT "a,b=":a,b
set point style 4
do
mouse poll x,y,L,R
if L=1 then
set point color 3
let x1=x+p
let y1=y+q
let t=angle(a,b)
let r=sqr(a^2+b^2)
plot points: x,y
set point color 7
plot points:r*(x1*cos(t)-y1*sin(t)),r*(x1*sin(t)+y1*cos(t))
else
plot lines
end if
loop until R=1
end
お絵描き3.BAS
set window -10,10,-10,10
draw grid
input prompt "a,b=":a,b
INPUT PROMPT "p,q=":p,q
set point style 1
do
mouse poll x,y,L,R
if L=1 then
set point color 3
let t=angle(a,b)
let r=sqr(a^2+b^2)
plot points: x,y
set point color 7
plot points:r*(x*cos(t)-y*sin(t))+p,r*(x*sin(t)+y*cos(t))+q
else
plot lines
end if
loop until R=1
end
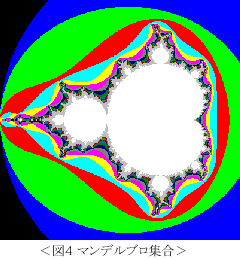
マンデンブロ.BAS
! マンデルブローのμ-map
! f(z)=z^2+μの反復が有界となる複素数μの集合
! μ=u+iv, z=x+iy ,f(z)=x1+iy1 とおくと,
! x1=x^2-y^2+u, y1=2xy+v となることを利用して複素数の計算を行う。
! x^2+y^2>4 であれば発散することを利用。
! さらに,そこに至るまでの繰り返し回数で色分けする。
OPTION ARITHMETIC NATIVE ! 二進演算
LET l = -2 ! left
LET r = .8 ! right
LET h = (r - l) ! height
SET WINDOW l, r,-h/2,h/2
ASK DEVICE SIZE px,py,s$
SET POINT STYLE 1
FOR u= l TO r step (r-l)/px
FOR v = 0 to h/2 step h/py
LET x = 0
LET y = 0
FOR n = 1 TO 250
LET x1 = x^2 - y^2 + u
LET y1 = 2 * x * y + v
LET x = x1
LET y = y1
IF x^2+Y^2>4 THEN
SET POINT COLOR MIN(n,15)
PLOT POINTS: u,v
PLOT POINTS: u,-v
EXIT FOR
END IF
NEXT n
NEXT v
NEXT u
END
円.BAS
picture circle !円の絵定義
set color mix(0) 0,0,1
set point color c
for x=0 to 2*pi step pi/10
plot points:cos(x),sin(x)
next x
end picture
set window -10,10,-2,18 !座標の設定
draw grid !グリッド(格子線)
def f(t)=t^2/6 !関数の定義
for t=-10 to 10 step 0.05 !ループ
let c=7
draw circle with shift(t,f(t)) !円の描画
let c=0
draw circle with shift(t-0.05,f(t-0.05)) !円の消去
next t
draw grid !グリッドの再描画
END