丂丂乥2x亅3乥亙x+I
偺夝傪媮傔傞偲偒丆塃曈偺惓晧偵傛偭偰応崌暘偗偡傞偙偲偼丆愨懳抣偺乽揰偐傜偺嫍棧乿偲偄偆暿掕媊偵傛傞傕偺偱偡偑丆偙偺偙偲偼姶妎揑偵偼妋偐偵偦偆偩偲巚偄傑偡丅幚嵺偵偼丆師偺傛偆偵帵偝傟傞偱偟傚偆丅
| 乥A乥亙B丆B亜0丂佁丂亅B亙A亙B丂乧乧(*)偺徹柧 |
丂偨偩丆妋偐偵偙偆徹柧偼偱偒傞偺偱偡偑丆愭惗傕偛巜棑偺捠傝B亝0偺応崌偼丆乥A乥亙B偼晄惉棫偱偡偐傜丆夝偼懚嵼偟傑偣傫丅
丂偙偺偲偒丆壖偵亅B亙A亙B傪擣傔偰偟傑偊偽丆B亙0偺偲偒偼丆0亙亅B丆A亙B亙0偲側傝傑偡偐傜丆嫟捠斖埻傪媮傔偰丆夝偼懚嵼偟側偄偙偲偲側傝傑偡丅
丂傛偭偰丆(*)偼丆
| 乥A乥亙B丂佁丂亅B亙A亙B |
ex1)乥x乥亙亅1偺偲偒丂1亙x丂and丂x亙亅1傛傝丆嫟捠斖埻傪峫偊偰夝偼側偄丅
偲側傝傑偡丅
丂側偍丆A丆B偑x偺1師幃偱偁傞偲偒丆偙偺偙偲偼丆僌儔僼偵傛傞夝摎偐傜梊憐偱偒傑偡乮偙偲傕愭惗偺偛堄尒偺拞偱怗傟傜傟偰偄偨偲巚偄傑偡丅乯
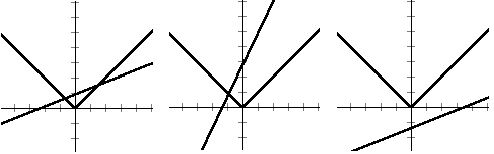
丂偄傑丆乥x乥亙mx亄n偲偟偰傕堦斒惈偼幐傢傟側偄偺偱丆y=乥x乥丆y=mx亄n偺埵抲娭學傪挷傋傞偲3偮偺Case偵応崌傢偗偱偒傑偡丅

丂偙偙偱丆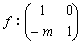 側傞1師曄姺傪峫偊傞偲丆
側傞1師曄姺傪峫偊傞偲丆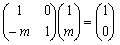 偲側傝丆捈慄偼丆x幉偵暯峴側捈慄偵曄姺偝傟傑偡丅
偲側傝丆捈慄偼丆x幉偵暯峴側捈慄偵曄姺偝傟傑偡丅
丂傑偨丆 偱偡偐傜曄姺倖偼倶偺抣偼曄偊偢偵偙傟傪奼懢丒弅彫偡傞偣傫抐偲偄傢傟傞偢傜偟曄姺偱偁傞偙偲偑傢偐傝傑偡丅廬偄丆偙偺曄姺偵傛偭偰傕丆傕偲傕偲偺愨懳抣晄摍幃偺夝偼曄傢傝傑偣傫丅幚嵺偵曄姺偟偨恾傪偦傟偧傟昤偔偲丆
偱偡偐傜曄姺倖偼倶偺抣偼曄偊偢偵偙傟傪奼懢丒弅彫偡傞偣傫抐偲偄傢傟傞偢傜偟曄姺偱偁傞偙偲偑傢偐傝傑偡丅廬偄丆偙偺曄姺偵傛偭偰傕丆傕偲傕偲偺愨懳抣晄摍幃偺夝偼曄傢傝傑偣傫丅幚嵺偵曄姺偟偨恾傪偦傟偧傟昤偔偲丆
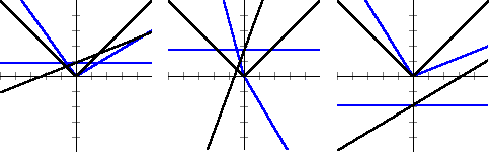
偲側傝傑偡丅偙偺傛偆偵丆塃曈傪悢抣壔偡傞偲丆揰偐傜偺嫍棧偲偄偆愨懳抣偺埖偄偑僋儘乕僘傾僢僾偝傟丆晧悢偺掕悢娭悢偵偍偄偰傕摨條偵張棟偱偒傞偙偲偑暘偐傝傑偡丅
丂偱偼丆乽亜乿偵偮偄偰偼偳偆偱偟傛偆偐丅偙偺応崌傕摨條偵寁嶼偱偒側偄偺偱偟傚偆偐丅
| 乥A乥亜B丂佁丂A亙-B丆B亙A |
|
| 乥A乥亙B丂佁丂亅B亙A亙B |
(仺)A亞O偺偲偒丆A亙B傛傝丆0亝A亙B丂偙偺傛偆偵峫偊傞偲丆B偺惓晧偵娭傢傜偢丆摨抣偑偄偊偰偟傑偆偱偼側偄偐偲巚偆偺偱偡丅偦偟偰丆掕媊偵傛傟偽丆A丆B偼1師偺惍幃偱偁傞昁梫偝偊側偄偺偱偡丅
丂A亙0偺偲偒丆亅A亙B傛傝丆亅B亙A亙0
丂傛偭偰丆2幃傪崌傢偣偰丆亅B亙A亙B
(仼)(*)偺徹柧偲摨偠
| 乥f(x)乥亙g(x)丂佁丂亅g(x)亙f(x)亙g(x) |
亅(x2亄5x)亙x亅3亙x2亄5x偲側傝傑偡丅
亅x2亅5x亙x亅3傛傝丆x2亄6x亅3亜0
偙傟偐傜丆丂乧嘆
傑偨丆x亅3亙x2亄5x傛傝x2亄4x亄3亜0
偙傟偐傜丆x亙亅3丆亅1亙x丂乧嘇
嘆偲嘇偺嫟捠嶚敓傪媮傔偰丆丂丂
丂摨條偵丆偙傟偐傜
| 乥f(x)乥亜g(x)丂佁丂f(x)亙亅g(x)丆g(x)亙f(x) |
丂偝偰丆偲偙傠偱丆乽傑側傇朄乿偺尷奅偵偮偄偰偱偡偑丆慜敿偺塃曈偑惓悢偵娭偟偰偼扤偟傕偦偺夝朄偵偼堎榑偺側偄偲偙傠偱偟傚偆丅
丂栤戣偼丆塃曈偑乽幃乿偵側偭偨応崌偱偡偑丆巹帺恎偼巜摫偺棳傟偲偟偰偼丆偙傟偼柧傜偐偵岆傝(岆杺壔偟)偩偲巚偭偰偄傑偡丅悢捈慄忋偵丆x偺2幃傪偲偭偰暲傋偰偄偔偙偲偽丆嫍棧偺堄枴偐傜偄偭偰傕僫儞僙儞僗偲偝偊巚偄傑偡(暘偐傝堈偄尒曽偐偳偆偐偼暿偵偟偰)丅乽傑側傉朄乿偺屻敿偼丆嫍棧偵傛傞掕媊偱偼側偔丆愨懳抣杮棃偺惓晧偵傛傞応崌暘偗偐傜摫偒弌偝傟偰偄傞偲偍偝偊偰偄傑偡丅傑側傉朄偺巜懜偱偼丆偦偙偺晹暘偑寚棊偟偰偍傝丆搑拞偱掕媊偺偡傝懼偊傪偟偰偟傑偭偰偄傞偺偱偡丅
丂偦偟偰丆偦偺杮棃偺愨懳抣偺掕媊偵傛傟偽丆塃曈偺惓晧偵傛傞応崌暘偗偼傕偼傗傑偭偨偔娭學側偄傛偆偵巚偊傞偺偱偡丅偦偙偺晹暘偑巹帺恎堷偭偐偐偭偰偍傝丆乽傑側傉朄乿偺尷奅偵偮偄偰丆愭惗曽偵搳偘偐偗偨棟桼偱傕偁傝傑偡丅
丂幚嵺偵丆堦斒偵庴尡嬈奅偱偼丆
丂丂乥f(x)乥亙g(x)丂佁丂亅g(x)亙f(x)亙g(x)
偵偮偄偰偼丆儅僯儏傾儖揑偵夝朄偑墶峴偟偰偄傑偡丅K幮傗T梊旛峑側偳偱偼偙偺夝朄傪傛偔尒偐偗傑偡丅偟偐偟丆
丂丂乥f(x)乥亜g(x)丂佁丂f(x)亙亅g(x)丆g(x)亙f(x)
偵偮偄偰偼丆偙傟傪擣傔偨夝朄偼偍栚偙偐偐偭偨偙偲偑偁傝傑偣傫丅堦庬丆僞僽乕帇偝傟偰偄傞偐偲媈偆傎偳偱偡丅
丂偦偺棟桼偼壗側偺偱偟傚偆丅摨抣偱偼側偄偲偄偆偙偲偑帵偝傟傟偽傕偪傠傫暘偐傝傑偡偑丆婣擺揑偵専徹偟偰偄偭偰傕丆摨抣惈偑曵傟偰偟傑偆傛偆側Case偑尒偮偐傜側偄偺偱偡丅ex2偺夝摎傪傒偰傕暘偐傞偐偲巚偄傑偡丅
丂偱偼丆惓偟偄偲偟偨偲偒偵壗屘丆偙偺夝朄偼巊傢傟側偄偺偱偟傚偆丅
丂巹尒偱偡偑丆偦偺応崌偼丆乽嫵堢揑攝椂乿偵傛傞傕偺偱偼側偄偐偲峫偊偰偄傑偡丅
丂傂偲偮偼丆応崌暘偗偺崿棎偱偡丅塃曈偑x偺惍幃偵側傞偲偒丆塃曈偺惓晧偵傛傞応崌暘偗偲愨懳抣傪偼偢偡嬒崌暘偗偑崿嵼偟偰偟傑偆偺偱偡丅偙傟偼惗搆傪崿棎偝偣傞偩偗偱偟傚偆丅
丂師偺棟桼偼丆夝廤崌偺奣擮偺棟夝偺擄偟偝偱偡丅偙偺愢柧偼旔偗傜傟偸偙偲偱偁傝丆榓廤崌丆愊廤崌偺抦幆偑梫媮偝傟偰偒傑偡偐傜丆1擭偺慜敿偺巜摫偱偼柍棟偑偁傞偺偱偼偲巚偆偺偱偡丅
丂偨偩丆巜摫傪旔偗偰捠偭偰傕傂偲偮戝偒側栤戣偑偁傝傑偡c 壖偵偙偺夝朄偑惓偟偄偲偟偨偲偒偵丆惗搆偑巜摫奜偲偟偰偙偺夝朄偱偺夝摎傪僥僗僩偱偟偨偲偟偨傜丆尰応偺愭惗偼丆偳偆懳墳偡傞偱偟傚偆偐丅夝摎偼仜側偺偱偟傚偆偐丆偦傟偲傕亊側偺偱偟傚偆偐丅
丂偙傟偑丆乽傑側傇朄乿偺夝摎偺尷奅偺戞2偺栤偄偐偗偵側偭偰偒傑偡丅
丂偦偟偰偙傟傜偺偙偲傪偡傋偰clear偝偣傞偲偡傟偽丆寢嬊僌儔僼偵傛傞夝朄偑best側傞偐偲巚偄傑偡丅
丂乽傑側傇朄乿偺夝朄偵偮偄偰偺堄尒偼丆恀撶愭惗偺懠偵丆峕暿崅峑偺彫嶳愭惗丆嶥杫堫杒崅峑偺憗昪愭惗偐傜傕偄偨偩偄偰偄傑偡丅
丂悢妛揑偵偼乽寉偄栤戣乿偱傕丆嫵堢揑偵偼乽巚偄栤戣乿偱偁傞偲巚偄傑偡偟丆偄傠偄傠側愭惗偐傜偛堄尒傪巉偊傟偼偲峫偊偰偄傑偡丅壞偺尋媶夛偱偼帪娫偑懌傝側偐偭偨偨傔偵愢柧偑尵梩懌傝偢偵廔傢偭偰偟傑偄丆昁偢偟傕愭惗偺偛幙栤丆偛堄尒偵摎偊偨宍偵側傜側偄夞摎偲側傝傑偟偨丅堷偒懕偒丆愭惗偺偛堄尒傪巉偊傟偽岾偄偱偡丅
|
乻丂娭丂楢丂帒丂椏丂乼
|