拞懞暥懃丂條
丂攓孾 愭惗偺儗億乕僩偼偄偮傕嫽枴怺偔攓尒偝偣偰偄偨偩偄偰偄傑偡丏愭擔偼悢幚尋偺壞婫僙儈僫乕偱偨偔偝傫偺柺敀偄榖傪暦偐偣偰偄偨偩偒桳傝擄偆偛偞偄傑偟偨丏崱擭偺4寧偐傜恑妛偱偄偊偽拞娫儗儀儖偺崅峑偵揮嬑偟丆愭惗偺儗億乕僩偼偲偰傕嶲峫偵側傝傑偟偨丏
丂崱夞偍曋傝偟偨偺偼丆偦偺拞偺乽愨懳抣晄摍幃偺儗億乕僩偵偮偄偰彮偟峫偊偰傒偨偺偱丆偦偺寢壥傪偛曬崘偟丆暪偣偰愭惗偺偛堄尒傪偆偐偑偍偆偲巚偭偨偐傜偱偡丏
1丏乽愨懳抣偺偮偄偨1師晄摍幃乿偵偮偄偰
丂愨懳抣偺婰崋 l l 傗愨懳抣偺偮偄偨曽掱幃丆晄摍幃偼惗搆偵偲偭偰(偦偟偰嫵巘偵偲偭偰傕)暘偐傝偵偔偄(嫵偊偵偔偄)晹暘偱偡丏偦偺揰偱偼丆愨懳抣偺拞偺幃偺抣偑尨揰偐傜偺嫍棧傪昞偡偲峫偊傞乽傑側傉朄乿偼丆捈姶揑偵傕傛偔暘偐傞曽朄偩偲巚偄傑偡丏巹傕偙偺曽朄傪梡偄偰栤戣傪夝偄偨宱尡偑偁傝傑偡丏
丂偝偰丆儗億乕僩偺慜敿偺3戣
丂丂丂(1)lx-3l亙4丆 (2)l2x-3l亙5丆 (3)l3x+4l亜2
偵偮偄偰偼乽傑側傇朄乿偼惓偟偄夝朄偩偲巚偄傑偡丏偟偐偟屻敿偺3戣
丂丂丂(1)l2x-3l亝x+1丆(2)l3x-1l亙x+3丆丂(3)lx-1l亞2x+3
偺傛偆側栤戣偵偮偄偰偼丆乽傑側傇朄乿偵偼晄廫暘側偲偙傠偑偁傞偲巚偄傑偡丏傛偔巜揈偝傟傞傛偆偵曽掱幃傗晄摍幃傪夝偔応崌丆昁偢摨抣娭學傪曐偮傛偆偵幃偵曄宍偟側偗傟偽側傝傑偣傫丏
丂椺偊偽丆愨懳抣偺偮偄偨幃側偳偱椉曈傪2忔偡傞偲丆摨抣娭學偑攋傟傞偙偲偑偁傞偐傜偱偡丏
丂慜敿偺3戣偺傛偆側栤戣丆偡側傢偪
丂丂丂乥ax+b乥亙k (a亜0丆k亜0偲偟傑偡)
偺傛偆側宆偺栤戣偱偼丆
丂丂丂乥ax+b乥亙k 偲 -k亙ax+b亙k
偲偼摨抣偱偡丏偲偙傠偑屻敿偺3戣偺傛偆側栤戣丆偡側傢偪
丂丂丂乥ax+b乥亙cx+d (a亜0丆c亜0偲偟傑偡)
偺傛偆側宆偺栤戣偱偼
丂丂 乥ax+b乥亙cx+d丂偲丂-(cx+d)亙ax+b亙cx+d
偲偼摨抣偱偼偁傝傑偣傫丏堦斒偵丆-(cx+d)亙cx+d偲偼側傜側偄偐傜偱偡丏摨抣娭學傪曐偮偵偼丆cx+d亞0偺応崌偲cx+d亙0偺応崌傪椉曽峫偊傞昁梫偑偁傝傑偡丏椺偊偽屻敿偺1斣栚偺栤戣偼師偺傛偆偵夝偔傋偒偩偲巚偄傑偡丏
丂(1) l 2x-3 l亝x+1
[夝]
(嘥)x+1亞0偺応崌 偡側傢偪 x亞-1丂乧丂嘆丂偺偲偒
丂梌幃偐傜
丂丂丂-(x+1)亝2x-3亝x+1
偱偡丏嵍曈偲拞曈偐傜 2/3亝x丆拞曈偲塃曈偐傜 x亝4丏
嫟捠斖埻偼 2/3亝x亝4丏偙傟偼忦審嘆傪枮偨偟偰偄傞偺偱丆寢嬊
丂丂丂2/3亝x亝4
偲側傝傑偡丏(嘦)x+1亙0偺応崌 偡側傢偪丂x亙-1丂乧丂嘇丂偺偲偒
丂梌幃偐傜
丂丂丂乥2x-3乥亝x+1亙0
偡側傢偪丆乥2x-3乥亙0偲側傝傑偡丏偲偙傠偑丆愨懳抣偺婰崋偺堄枴偐傜丆
偮偹偵 乥x-1乥亞0 偱偡丏偙傟偼柕弬丏偮傑傝丆忦審嘇偺傕偲偱偼梌幃傪枮偨偡x偺斖埻偼偁傝傑偣傫丏
偟偨偑偭偰丆(嘦)偺応崌偼峫偊傞昁梫偼側偔側傝傑偡丏(嘥)丆(嘦)偐傜傕偲傔傞夝偼
丂丂丂2/3亝x亝4 偲側傝傑偡丏
(2)乥3x-1乥亙x+3 傕摨條偵丆x+3亞0偺応崌偩偗傪峫偊傟偽傛偄偺偱丆寢嬊摎偼乽傑側傇朄乿偱媮傔偨傕偺偲乕抳偟傑偡丏
(3)乥x-1乥亞2x+3 偼師偺傛偆偵夝偒傑偡丏
[夝]
(嘥)2x+3亞0偺応崌 偡側傢偪 x亞-3/2 乧丂嘆偺偲偒
梌幃偐傜
丂丂丂x-1亝-(2x+3)丂傑偨偼 丂2x+3亝x-1丏
偦傟偧傟傪夝偄偰
丂丂丂x亝-2/3 傑偨偼 x亝-4 偱偡丏
忦審嘆偲崌傢偣偰丆
丂丂丂-3/2亝x亝-2/3 偲側傝傑偡丏(嘦)2x+3亙0 偺応崌 偡側傢偪 x亙-3/2丂乧丂嘇 偺偲偒丆
丂丂丂2x+3=堦k (k亜0)偲偍偔偙偲偑偱偒傑偡丏梌幃偐傜
丂丂丂乥x-1乥亞-k
偲側傝傑偡偑丆愨懳抣偺堄枴偐傜丆梌幃偼偡傋偰偺x偺抣偵懳偟偰惉傝棫偪傑偡丏
忦審嘇偲崌傢偣偰丆
丂丂丂x亙亅3/2 偱偡丏(嘥)丆(嘦)偐傜傕偲傔傞夝偼
丂丂丂x亝-2/3 偲側傝傑偡丏
丂寢嬊丆摎偼乽傑側傇朄乿偱媮傔偨傕偺偲乕抳偟傑偡偑丆晄廫暘側偲偙傠偑偁傞偙偲偑傢偐傝傑偟偨丏
丂榖傪傑偲傔傞偲丆乽愨懳抣偺偮偄偨1師晄摍幃乿偱偼乽傑側傇朄乿偑桳椡側夝朄偱偁傞偙偲偑傢偐傝傑偟偨偑丆巹屄恖偲偟偰偼丆僌儔僼偵傛傞夝朄偑傢偐傝堈偔岲偒偱偡丏
2丏僌儔僼偵傛傞乽愨懳抣偺偮偄偨1師晄摍幃乿偺夝朄
丂師偺傛偆側晄摍幃傪峫偊傑偡丏
丂丂丂乥ax+b乥亙cx廫d (a亜0丆c亜0偲偟傑偡)
偙傟傪丆
丂丂丂丂y1=乥ax+b乥
丂丂丂丂y2=cx+d
偲偍偄偰丆僌儔僼傪偐偄偰 y1亙y2傪枮偨偡x偺斖埻傪傕偲傔傑偡丏
丂堦斒偵丆y1=乥ax+b乥偺僌儔僼偼V帤宆偺僌儔僼偵側傝傑偡丏

丂y2 =cx+d 偺僌儔僼偼1師娭悢偺捈慄偺僌儔僼偱偡偐傜 y21亙y2 傪夝偔偨傔偵偼丆2偮偺僌儔僼偺埵抲娭學(岎揰)偑廳梫偵側傝傑偡丏偙傟偼師偺傛偆偵丆戝偒偔3偮偺僞僀僾偵暘椶偱偒傑偡丏
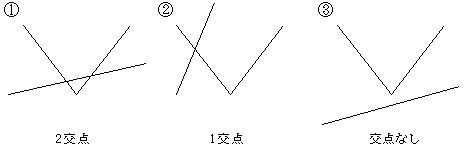
丂僌儔僼偑偐偗傟偽丆屻偼岎揰傪寁嶼偟偰丆忦審傪枮偨偡x偺斖埻傪傕偲傔傟偽傛偄傢偗偱偡丏屻敿偺栤戣偱偼丆(1)偲(2)偼嘆偺僞僀僾丆(3)偑嘇偺僞僀僾偵側傝傑偡丏
丂埲忋丆幹懌傪彂偒楢偹傑偟偨偑丆愭惗偺偛堄尒傪偆偐偑偊傟偽偲巚偭偰偍傝傑偡丏
丂愭惗偺偛寬彑傪偍婩傝怽偟忋偘傑偡丏
1998擭8寧14擔 恀戔榓峅丂丂
| 乻丂娭丂楢丂帒丂椏丂乼 |