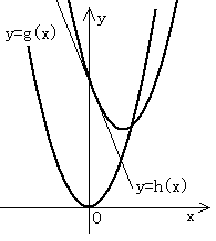
２次関数 を和関数とみて
　　　　
と分解する。これから、二次関数の一般形のグラフは、直線（標準形）の上に、２次関数の基本形の値を加えていけば描かれる。このとき、のとき、であるから、直線のグラフの上方に、２次関数は描かれ、唯一，のとき、は共有点をもつ。すなわち、はにおけるの接線となる。の場合も同様のことがいえる。このことから、１次の係数bの図形的意味を読み取ることができる。

　上の点(１,a)の変化により、aはグラフの開きを表す。また、cはy切片である。さて、１次の係数bについては、和関数の考え方により、はの接線よりにおけるの接線の傾きである。

以上のことより、 のグラフは、直線 を描き、グラフの開きがaである二次関数をで接するようにの上に乗せる（下にぶらさげる）と出来上がる。

解説) グラフは上に凸よりa＜０，放物線とx軸の交点が正より、c＞０，

また、x＝０におけるの接線を引くと、その傾きは正であるから、b＞０である。
　以上より、の各項の係数の符号を求めると、
　　　　　　　

Ｎｏｔｅ)

　 とすると より、よって､における接線は となる。

　あるいは、 と との交点を求めると、yを消去して､ これから、(重解)となるから接する。

　このように、判別式や微分を利用すると、bの図形的な意味は容易に分かるのだが、二次関数の単元を指導する上ではこのような接線の考え方は無理がある（どちらの考え方も後の単元で触れるわけであるから）。だから、２次関数を直線との和関数とみることにより、直線に放物線が置かれた(乗っかった)状態を接すると考え、感覚的に接線の意味を理解させるだけで十分であろう。

　次に、接線 の図形的な意味を、もっと別角度で考えてみよう。
　　　　　とすると　　　　
となる。このとき、一次変換ｆによりのグラフは、x座標は変えずに、y軸方向に（原点を変えずに）引っ張った形で変換される。この１次変換を、せん断（スケーリング）という。このとき、基本ベクトルに変換されるから直交座標上の点はで作られる斜交座標系に移される。この斜交座標上でy軸方向にcだけ平行移動すれば、のグラフとなる。すなわち、
　　　　
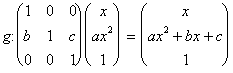
とみると、２次関数の基本形から一般形への変換は、アフィイン変換ｇと考えればよい。また、であり、平行移では平面上の図形の面積は不変であるから、この変換は等積(等面積)変換とみることもできる。

　　これを利用すると、次のような放物線と直線が囲む面積問題が簡単に解ける。

解説）

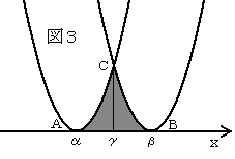
図１、図２はいずれも図３を等積変換したものであることは明らかである。よって図１と図２の斜線部分の面積は、図３の面積に等しい。

図１、図２のグラフの開きをaとすると、図３の２つの関数はそれぞれ
　　　　　
とおくことができる。また、図３より明らかに
　　　　
よって、これから求める面積Ｓは、
　　　　
　　　　　　
　　　　　　
　　　　　
　　　　　
　なお、図１の面積をＳ_１とすると、線分AB（極線）と放物線で囲まれる部分の面積は、 より、
　　　　　Ｓ_１：Ｓ_２＝１：２
であることが分かる。