和関数としての３次関数
次に、３次関数のグラフを、和関数を利用して素描することを考えていこう。
２次関数と同様に、３次関数 
の、各項の係数のグラフ確定要素としての意味を調べてみる。
より
これから各項の係数は、x＝０においてそれぞれ次の役割をもつことがわかる。
定数項ｄはy切片、１次の項cは
の接線の傾き（すなわち、
は、x＝０における
の接線の方程式である）また、２次の項bは、
のy軸（の近傍）におけるグラフの凹凸を表している。
このことを利用すると、x＝０におけるグラフの状態から３次関数の各項の係数の符号を判断することが可能となる。
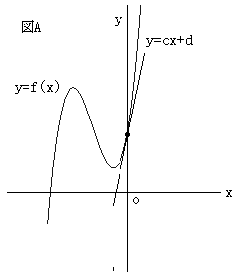
たとえば、右図Aのグラフ 
は、x＝０における交点のy座標（y切片）、接線の傾き、グラフの凹凸より、ｄ＞０，c＞０，b＞０、また、
であるから、a＞０となる。
このように、グラフのy軸での状態やグラフの開きをみることにより、３次方程式の各項の係数の符号を容易に求めることができるが、しかし、このことはグラフの素描には必ずしもつながらない。３次関数 
が与えられたとき、係数の符号から判断できることは、グラフの開き具合、y軸近傍のグラフの状態と、ほんの僅かな情報に限定されているのである。
そこで、２次関数同様に、３次関数についても和関数を利用し、２つの関数に分解することで概形を調べてみよう。
３次関数を次のように２つの関数に分解する。
このとき、
は、x＝０における
の接線の方程式である。
また、
、 
であるから、
は原点で接し、x軸と
で交わり、
で、極値をとるグラフである。
この
のグラフを直線
のグラフに、和関数と考え、x＝０で接するように乗せる（ぶら下げる）と
のグラフが出来上がる。だが、実際にはこれだけでグラフの概形を捉えることは難しい。
放物線が和関数を利用して容易にグラフが描けたのは、
にx軸で接することさえ理解すれば、グラフの開きが同じ放物線を描けばよいのである。だが、３次関数の場合は、和関数とみても、
は不確定要素の係数を２つ有し、単純に
として点をプロットすることはできない。
そこで、３次関数の次の性質を利用してみよう。
さて、
を分解して得られる 
の変曲点を求めると、
より、
、 
∴ 変曲点は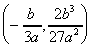
である。
この変曲点に 
の値を加え、点をy軸方向にスライドさせると
の変曲点となる。そうして、
のグラフを、x＝０で
に接し、さらに変曲点で点対称になるように描けばいいわけである。
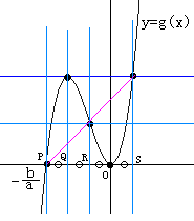
ところで、
とx軸との交点の座標をＰ、原点以外の極値、変曲点からx軸へ下ろした垂線の足をそれぞれＱ、Ｒとすると、
Ｐ
，Ｑ
，Ｒ
であるから、４点Ｐ、Ｑ、Ｒ、Ｏ（原点）は等間隔に並ぶ。さらに、変曲点における点Ｐの対称点からx軸に下ろした垂線の足をＳとすれば、この点も４点と同じく等間隔に並ぶのは明らかである。
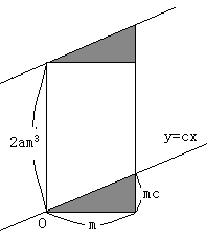
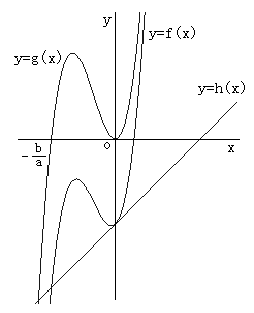
これから３次関数
は、x軸およびx軸に平行で変曲点、頂点を通る直線と、y軸およびy軸に平行で点Ｐ，Ｑ，Ｒ，Ｓを通る直線により、８つの合同な長方形上に分割されることになる（右上図）。
ここで、
とおくと、
であるから、長方形の２辺の長さの比は、１：２aｍ２である。よって、
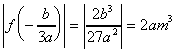
のグラフは点Ｐの位置（曲線とx軸との交点）さえ分かれば、８つの長方形をアウトラインとして、頂点、変曲点を押さえて簡単に描くことができる。
さらに、
は、x軸を 
に移す等積変換であることを利用すると、８つの合同の長方形は等面積の平行四辺形に変換される。各点Ｐ，Ｑ，Ｒ，Ｓの間隔は不変であり、y座標の値も一定数の加算であるから、長方形と平行四辺形のy軸方向の辺の長さは等しい（右図）。
以上のことを踏まえ、
の素描法についてまとめてみよう。
① 
の変曲点を求め（x軸と
の交点をＰとすると、線分ＯＰを１：２の比に内分する点が変曲点のx座標Ｒである）、和関数により、
の値を加えて
の変曲点を求める。
② 直線
に平行で、
の変曲点を通る直線ｇを引き、この直線ｇに対して
の反対側に、ｇに平行で等間隔になるように直線を引く。
③変曲点を通りy軸に平行な直線を引き、その直線を軸として、ＯＲの長さで等間隔になるように両側にy軸に平行な直線を２本ずつ引く。
④８つの平行四辺形をアウトラインとして、変曲点で点対称になるように 
のグラフを描いていく。
Ｎｏｔｅ）
は等積変換であるから、８つの長方形と曲線によって分割された各部分の面積は
上の平行四辺形においてもその面積は保存される。
，
として計算してみよう。
とすると、
であるから
図形の面積を下図のようにおくと、
，
，
，
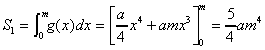
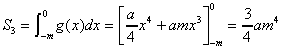
よって、
となる。
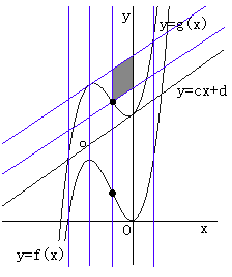
さて、
から等積変換により 
を生成しても、その面積は不変であるから、下右図のような面積比が得られることになる。
ここで、直線 
と放物線 
で囲まれる部分の面積Ｓは、
であたえられる。
なお、一般に、
は、その変曲点を通り、
と、変曲点以外の２点で交わる直線と、その直線に平行で、
に接する２つの直線によって、前述したのと同様の方法により、等面積の８つの平行四辺形に放物線は分割される。
Ｎｏｔｅ）
すべての３次関数がその変曲点において、点対称であることは、変曲点をとるx座標を中心(極)にしてＴａｙｌｏｒ展することにより示されるが、和関数の考えでは、
について、確認すれば十分であろう。
の変曲点は、
であるから、変曲点が原点になるように
を平行移動すると、
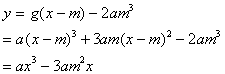
より奇関数となり、原点対称であることがわかる。よって、変曲点において、点対称であることがわかる。