友円数について
三角形の３辺の長さが自然数値で与えられていて、角の大きさの１つが（代数的に）求められるとき、その３辺の組を友円数と定義しよう。直角三角形の３辺になれる３つの自然数の組をピタゴラス数というが、ピタゴラス数は、斜辺の対角が90°であるから友円数である。もちろん上述の組 (a,b,c)も友円数である。
実際、三角関数で値が求められる角度は限定されている。余弦定理より、
であるから、a,b,cが自然数であれば、cosCは有理数となる。よって、
C=60°，90°，120°
となる。C=90°の場合がピタゴラス数であるから、C=60°，120°として考えてよい。
以上より、
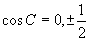から、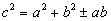
の自然数解が友円数となる。
友円数と三角形の外接円との関係
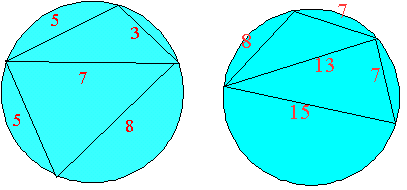
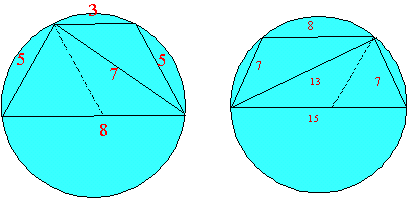
(a,b,c)=(3,5,7),(5,8,7)である三角形とその外接円との関係を調べてみよう。
辺 c＝７の対角は、それぞれ120°,60°であることより、これらの角は、補角の関係から辺cを弦とする円の円周角である。
(a,b,c)=(8,7,13),(15,7,13) についても、辺c＝13を弦として同様のことがいえるから、２つの三角形は図のように円に内接させることができる。
さらに配置を変えると、
すなわちいずれも円の内部で三角形を組み合わせると等脚台形となり、さらに台形は、正三角形と平行四辺形に分割される。この位置関係を利用して友円数を求めてみよう。
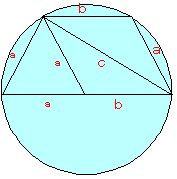三角形に余弦定理をあてはめ、
c2=a2+b2−2abcos120°
＝a2+b2+ab
同様に、
c2=a2+(a+b)2−2a(a+b)cos60°
＝a2+a2+b2+2ab−a(a+b)
＝a2+b2+ab
よって、友円数は、c2＝a2+b2+ab の整数解であり、(a，b，c) と(a，a+b，c)が対で現れる。
では、その整数解を求めてみよう。
c2 = (a+b)2−ab より、ab = (a+b)−c2 = (a+b+c)(a+b−c)
a+b+c＝k とおくと、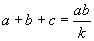 
この２式を辺々加えて、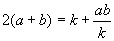
2ka+2kb−ab=k2 a(ak−b)−2k(2k−b)=−3k2(a−2k)(b−2k) = 3k2
ここで、例えば、a−2k =3，b−2k＝k2とおくと、
a=2k+3，b=2k+k2となる。
さらに、k＝m−1とすると、
a＝2m＋1，b＝m2−1
c＝a＋b−k＝(2m＋1)＋(m2−1)−(m−1)＝m2＋m＋1 となり、
(2m＋1)2＋(m2−1)2＋(2m＋1)(m2−1)＝(m2＋m＋1)2 が成立する。
mに適当な値を代入して、
m＝2 のとき、(a，b，c)＝(5，3，7)， (a，a＋b，c)＝(5，8，7)
m＝3 のとき、(a，b，c)＝(7，8，13)， (a，a＋b，c)＝(7，5，13)
m＝5 のとき、(a，b，c)＝(11，24，31)， (a，a＋b，c)＝(11，35，31)
m＝7 のとき、(a，b，c)＝(15，48，57)＝(5，16，19)，
(a，a＋b，c)＝(5，8，7)＝(5，31，19)
となり、新たな友円数が見つかった。