代数幾何学による一般的解法

　初等整数論（ピタゴラス）的な解法に対して、代数幾何(ディオファントス)的証明を以下に示そう。

　　　a²+b²+ab=c²の両辺をc²で割り、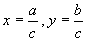とおくと、

　　　x²+xy+y²=1 ………（＊）

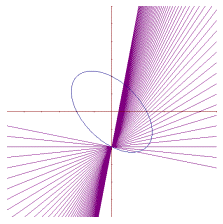　よって、友円数は、二次曲線（楕円）上の第１象限における有理点を考えればよいことがわかる。

（＊）上の１点Ａ(０,−１) を通る直線をy=tx−1とする。

　この直線が再び曲線（＊）と交わる点Ｂを求めてみよう。

　（＊）に代入して、

　　　x²+x(tx−1)+(tx−1)²=1

　　　(t²＋t＋1)x²−(2t＋1)x＝0

　　　x{(t²＋t＋1)x−(2t＋1)}＝0

　　　　∴

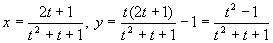
　以上より、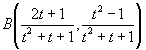となる。

　ここで、点Ａを通る直線の傾きを有理数の範囲で変化させ、二次曲線上をスキャンしていくと、有理点に対応した友円数が現れてくることがわかるだろう。

　では、点Ｂ以外の有理点の存在について次に調べてみよう。

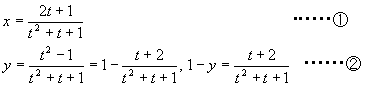
より、�@，�Aを辺々割って、

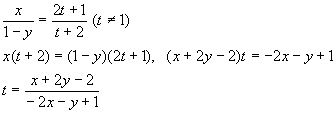
これから、x，yが有理数ならば、tも有理数である。

　また、tが有理数ならば、明らかに点Ｂは有理点である。よって、二次曲線上のすべての有理点は、点Ｂで表現される。そこで、

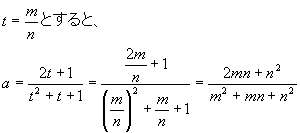
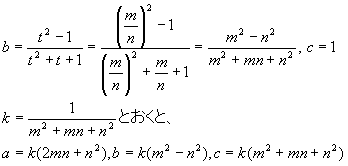
が友円数の一般解となる（求角120°に対しての）。