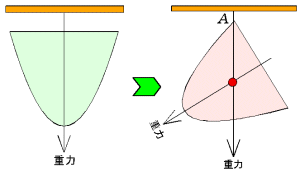
閉曲線で囲まれた図形が密度が一様な薄い素材(重さが面積に比例するということ)で作られている場合、その重心は、重力方向の釣り合いを２箇所実測できれば求められる。例えば右図の放物線の重心について考えるとまず図形の対称性から軸上に重心は存在する。次に端点のひとつである点Aに糸を括りつけて放物線を吊るすと、その重力方向にも重心は存在するから、放物線の軸と交わる点が重心となる。この糸により、図形の面積は二等分されるから、重心は、図形の面積を二等分するような２直線の交点である。
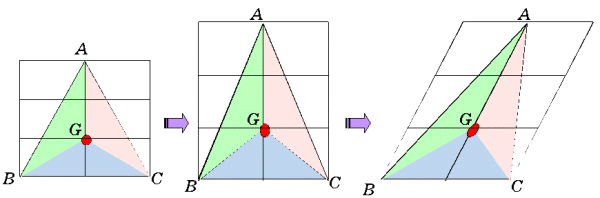
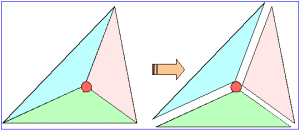同様に三角形の重心も求められるが、重心をvalance-pointとみると、三角形がその内部の点により３つの等面積の三角形に分割されるとき、その点が重心である。このことは正三角形の一次変換による像を見ることで簡単に確認できる。正三角形ABCの頂点Aから対辺に下ろした垂線を２：１に内分する点をGとすると、△ABC＝３△GBC, △GAB=△GCAより、△GAB=△GBC=△GCAであるからこの点Gが重心である。次に、適当に上下の方向に三角形を拡大・縮小し、さらに、左右の方向にスケーリング(せん断)することで任意の三角形を表現することができる。この変換によって、面積比、線分比は不変であるから以上より三角形の重心は中線を２：１の比に内分する点である。
また、頂点A以外についても同様の操作ができることより三角形の重心は中線の交点ともいえる。
