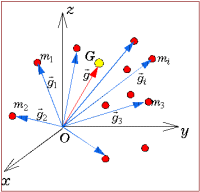
 慣性系における重心は、図形を構成する点に同量の重さ(慣性質量)を加えたときの平均であり、質量中心とも呼ばれる。すなわち慣性系ではすべての慣性質量が凝集した点(連続した質点の集合体としての剛体も含めて)を重心という。いま、質点の位置ベクトルと慣性質量をそれぞれ
慣性系における重心は、図形を構成する点に同量の重さ(慣性質量)を加えたときの平均であり、質量中心とも呼ばれる。すなわち慣性系ではすべての慣性質量が凝集した点(連続した質点の集合体としての剛体も含めて)を重心という。いま、質点の位置ベクトルと慣性質量をそれぞれ 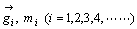 とすると、重心
とすると、重心  は
は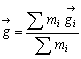
で与えられる。(これは統計学における加重平均を表している。)
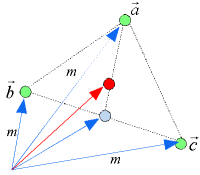 三角形の重心は、3つの頂点に同量の重さがかかったときの平均である。頂点の位置ベクトルを
三角形の重心は、3つの頂点に同量の重さがかかったときの平均である。頂点の位置ベクトルを 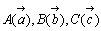 とし、慣性質量をmとすると、重心の位置ベクトル
とし、慣性質量をmとすると、重心の位置ベクトル  は、
は、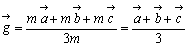
となる。ここで、
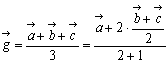
とみれば、重心は、頂点Aと線分BCの中点Mを結ぶ線分AMを2:1の比に内分する点であり、幾何的重心と一致することが分かる。
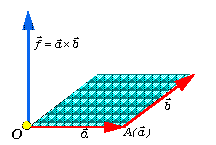 では、質点を表す三角形の頂点の慣性質量が異なる場合の重心はどうなるだろう。moment(能率、回転力)の原理を利用したvalance-methodなる方法により説明してみよう。
では、質点を表す三角形の頂点の慣性質量が異なる場合の重心はどうなるだろう。moment(能率、回転力)の原理を利用したvalance-methodなる方法により説明してみよう。momentとは、慣性系において、質点
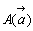 に加わる力を表すベクトル
に加わる力を表すベクトル 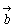 に対し、その外積
に対し、その外積 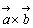 で与えられる。すなわち、ベクトル
で与えられる。すなわち、ベクトル 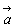 ,
,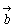 を二辺とする平行四辺形の面積を大きさとし、
を二辺とする平行四辺形の面積を大きさとし、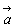 から
から 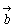 へ向かう方向を右ねじとして平行四辺形に垂直な方向をもつベクトル
へ向かう方向を右ねじとして平行四辺形に垂直な方向をもつベクトル 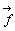 のことである。このとき、質点Aには、ベクトル
のことである。このとき、質点Aには、ベクトル 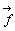 を回転軸として、
を回転軸として、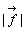 の大きさの回転力が働く。したがって、moment(瞬間、原語はねじれの意)は、回転力の度合いを表していることになる。
の大きさの回転力が働く。したがって、moment(瞬間、原語はねじれの意)は、回転力の度合いを表していることになる。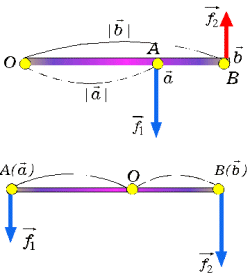 momentを、剛体上で考えると図のように端点に始点をとると、A, Bでの回転力の大きさが等しいとき(向きは逆)、剛体は釣り合う。これから、
momentを、剛体上で考えると図のように端点に始点をとると、A, Bでの回転力の大きさが等しいとき(向きは逆)、剛体は釣り合う。これから、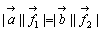 より、
より、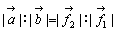 が得られる。また、剛体上での始点が図のようにその内部にあるときは、
が得られる。また、剛体上での始点が図のようにその内部にあるときは、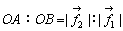 であるから、始点Oの位置ベクトルは
であるから、始点Oの位置ベクトルは 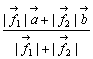 とも表される。ここで、
とも表される。ここで、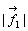 ,
,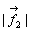 はそれぞれ質点A, Bにオモリをぶら下げたときの重さと考えればよい(剛体に質量はないとする)。
はそれぞれ質点A, Bにオモリをぶら下げたときの重さと考えればよい(剛体に質量はないとする)。逆に、2つの質点にオモリをぶら下げたときにその始点(着力点)は、質点間に一意的に定まってくる。このように質点間に逐次、始点(支点といった方適切であろう)でvalanceをとりながら、質点全体の中心(重心)を辿っていく方法をvalance-methodという。
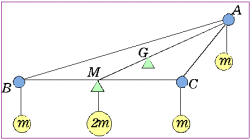 これを三角形ABCで考えてみよう。各頂点A, B, Cにそれぞれmのオモリをぶらさげるとき、辺BC上の支点はその中点Mであり、重さ2mが加わる。次に線分AM上ではAG:GM=2:1となる点Gが支点、すなわち重心となる。
これを三角形ABCで考えてみよう。各頂点A, B, Cにそれぞれmのオモリをぶらさげるとき、辺BC上の支点はその中点Mであり、重さ2mが加わる。次に線分AM上ではAG:GM=2:1となる点Gが支点、すなわち重心となる。 では、各質点にぶら下げるオモリを変えるとどうなるだろうか。
頂点
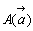 ,
,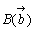 ,
,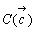 にそれぞれ、3,2,1のオモリをぶら下げてみよう。
にそれぞれ、3,2,1のオモリをぶら下げてみよう。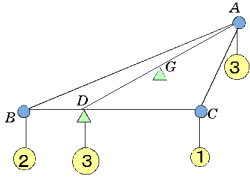 辺BC上の支点
辺BC上の支点 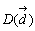 は、BD:DC=1:2なる点であるから、
は、BD:DC=1:2なる点であるから、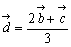
さらに、線分AD上の支点
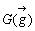 の回りのmomentを考えると、Dには3の重さが加わるから、AG:GD=1:1より、
の回りのmomentを考えると、Dには3の重さが加わるから、AG:GD=1:1より、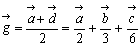
となる。
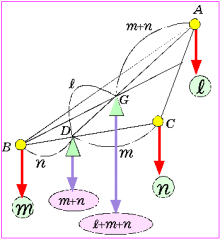 一般に、三角形ABCの3頂点の慣性質量をそれぞれl, m, nとするとき、辺BC上でmomentを考えると、BD:DC=n:mとなる点 が支点となり、支点にはm+nの重みが加わり、
一般に、三角形ABCの3頂点の慣性質量をそれぞれl, m, nとするとき、辺BC上でmomentを考えると、BD:DC=n:mとなる点 が支点となり、支点にはm+nの重みが加わり、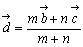
である。次に線分AD上でmomentを考えると、AG:GD=m+n:lとなる点 が支点であり、
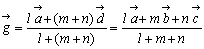
が得られ、前述の質量中心の結果に一致する。
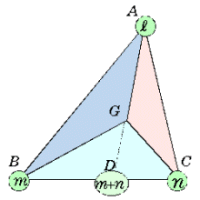 このとき、△ABCの面積をl+m+nとすると、AG:GM=m+n:lより、
このとき、△ABCの面積をl+m+nとすると、AG:GM=m+n:lより、△GBC=l, △GAB+△GCA=m+n
である。また、△GAB:△GCA=BD:DC=n:mより、△GAB=n, △GCA=mであるから、
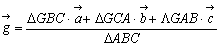
となり、幾何的重心についても加重を考えることが可能となる。