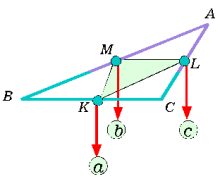
辺BC,CA,ABの中点をそれぞれK, L, Mとすると、各中点に加わる慣性質量は辺の長さに比例するから、a,b,cとしてよい。したがって、右図の三角形KLMの加重平均を求めればよい。よって重心 
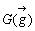は、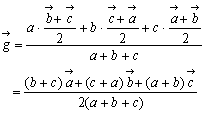
となる。
ではこの重心Gはどんな点を表しているのだろうか。
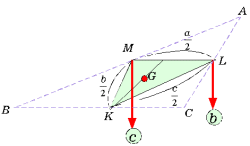線分LMにおけるモーメントを考えると、辺LMの支点Pは、LMをb：cの比に内分する点である。また、三角形KLMの各辺の長さは二辺中点連結定理より、
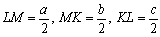
であるから、MP：PL=b：cより、KM：KL=MP：PL。よって、線分KPは∠MKLの二等分線となる。これからフレーム三角形の重心は、三角形ABCの辺の中点を結んで作られる三角形の内心に一致する。さらに、
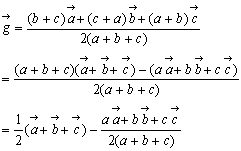
である｡
ここで、三角形ABCの重心を 
とすると、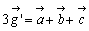
である。
また、三角形ABCの内心
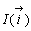の位置ベクトルは、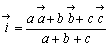
であることより、
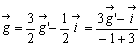
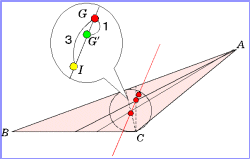
よって、フレーム三角形の重心は、線分 IG' を３：１の外分する点であるといえる。