物理的重心は、四角形ABCDの各頂点 
,
,
,
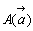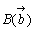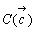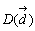に同量のオモリをぶら下げたときの平均より重心 
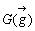は、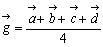
である。ここで
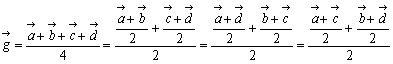
とみれば、バランスをとる順番により重心の位置表現は異なるが、４頂点のうち、２頂点ずつの組から作られる２線分の中点を結ぶ線分の中点が重心といえる。
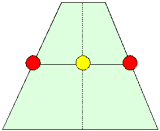また、各辺AB,BC,CD,DAの中点をそれぞれK,L,M,Nとすると、四角形KLMNは平行四辺形であり、その対角線の交点が四角形ABCDの重心でもある。次に均質な材料で作られた板状の四角形の幾何的重心であるが、必ずしも４点の重心に一致はしない。例えば、右図のような台形では物理的重心によって面積が二等分されないのは明らかなことである。これは質点系における４点では四角形が決定しないことを意味している。４点で作られる直線図形には左図のようなものも含まれ、これらに対しても物理的重心がその平均として得られる。したがって、図形の外部に重心が存在することもありえるのである。
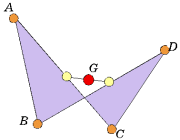しかし、空間内で考えれば、４点を結んで得られる直線図形は、四面体を形成する。すなわち、物理的重心は次元において確定するものと考えればよい。そしてこのときに、物理的重心と幾何的重心は一致する。
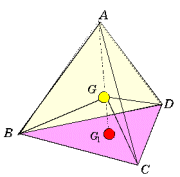実際、重心Gの位置ベクトルは、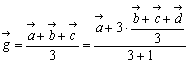
とみることで、三角形BCDの重心を G1とすると、線分AG1 を３：１の比に内分した点であることがわかる。ここで、四面体GBCDの体積 V1は、四面体ABCDの体積Vの 1/4 倍である。同様に、その他の頂点B,C,Dとそれぞれの対面である三角形の重心を結ぶ線分を３：１の比に内分する点が重心Gでもあるから、四面体GACD,GABD,GABCの体積 に対して、
V1=v2=v3=v4=V/4
が成立し、均質な材料で作られている内部の詰まった四面体は、その重心Gにより、４つの体積の等しい(すなわち重さの等しい)四面体に分割される。
以下、質点の個数に応じて、４次元、５次元と次元を拡張していけば、その次元に対して物理的重心と幾何的重心は一致することが予想される。では、平面図形としての４点で作られる板状の四角形の重心の位置を探してみよう。
計測としては、四角形を重力方向に吊り下げることで重心を求めることは可能であるが、momentの釣り合いを利用すると作図として求めることができる。
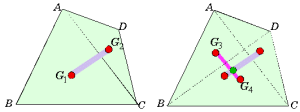四角形ABCDをその対角線ACにより、２つの三角形、△ABC, △ACDに分ける。そのそれぞれの重心を
,
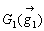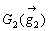
とすると、質点 G1,G2 の質量中心が求める重心であり、線分 G1G2 上に存在する。また、対角線BDによって分けられる三角形の重心 G3,G4 を結ぶ線分上にも重心は存在するから G1G2 との交点が四角形の重心である。
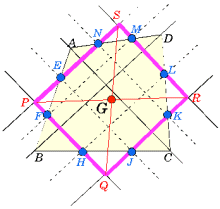ところで、四角形の物理的重心は各辺の中点を結んでできる平行四辺形の交点であったが、同様に幾何的重心についても平行四辺形の交点として求めることができる。コクセター著「幾何学入門」の中に次のような記述がある。
四角形の４つの辺の３等分点を通る四角形を作ると、この四角形は平行四辺形である。このとき、その対角線の交点が幾何的重心となる。
その証明は次のように考えればよい。
線分EJ, KNの中点は三角形ABC, 三角形ACDの重心であるから２中点を結ぶ線分上に四角形の重心はある。 同様に、線分MF, HLの中点を結ぶ線分上にも重心があるから、２線分の交点が四角形の重心である。
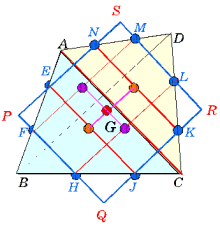一方、この重心が平行四辺形PRQSの対角線の交点であることは明らかなことである。なお、四角形の４辺の中点から作られる四角形はヴァリニュン(Varignon)の平行四辺形、４辺の３等分点から作られる四角形はウィッテンバウアー(Wittenbauer)の平行四辺形とよばれる。