【TOP】 【BACK】 【NEXT】

　次に四角形の重心の位置をカバリエリの原理を使ってもう少し探ってみよう。

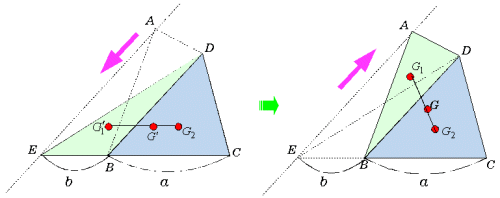
　図中、四角形ABCDの頂点Aを対角線BDに沿って、平行にスライドさせ、BCの延長と交わる点をEとする。ここで三角形DEB, 三角形DBC, 三角形DECの重心 G₁',G₂,G' を求め、もう一度、点Eを対角線BDに沿ってスライドさせ、点Aに戻すと点 をスライドした点Gが求める重心となる。

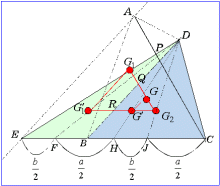　３重心 G₁,G₂,G の関係を調べてみよう。
　BC=a,BE=bとする。△DEB,△DEC,△DBCの頂点Dから対辺に引いた中線と対辺との交点をF, H, Jとする。
　EF=FB=b/2，EF=HC=(a+b)/2，BJ=JC=a/2より、
　　　EF=EH-EF=a/2，HJ=CH-CJ=b/2
である。
　ここで、３点 G₁',G',G₂ は中線を２：１の比に内分する点であるから、３点は一直線上にあり、G₁'G₂ // EC である。
　また、G₁G₁' // GG' でもあるから、
　　　G₁G:GG₂=G₁'G':G'G₂=EF:HJ=a:b
となる。さらに、辺DBと線分 G₁G₂,G₁'G₂ との交点をQ,Rとすると、
　　　FB=HJ=b/2
であるから、G₁'R=G'G₂,G₁Q=GG₂ を得る。
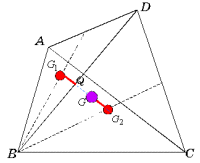これから四角形の重心は次のように求めればよい。
　まず、対角線により四角形を２つの三角形に分け、その各々の重心 G₁,G₂ を求める。線分 G₁G₂ と対角線との交点をQとし、G₁Q2Q であれば、G₁Q=G₂Q となる点Gを線分 G₂Q 上にとると、Gが四角形の重心である。

【TOP】 【BACK】 【NEXT】