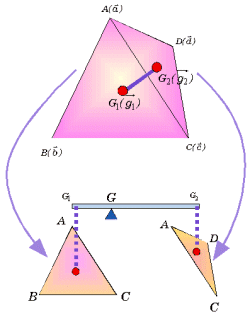
さて、これで重心のひとつの作図法が得られたわけであるが、この重心は、対角線の交点Pとも深い関わりをもっている。それは、AE//DBであることより、AP:PC=EB:BC=b:a
よって、
G1G:GG2=PC：AP
となることが予想される。質量中心Gは、質点 G1,G2 を両端とする線分上に存在するが、端点の慣性質量は点Pによって決定する。このことを説明しよう。
四角形ABCDを対角線ACにより２つの三角形ABC,三角形ACDに分け、そのそれぞれの重心を
, 
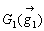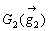とする。四角形の重心 
の位置ベクトルは、線分 G1G2 の端点に△ABC,△ACDの面積に比例する重みを加えたときの支点の位置にある。よって、G1G:G2G=△ACD△ABC
である。これから、
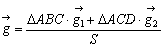(Sは四角形ABCDの面積) 
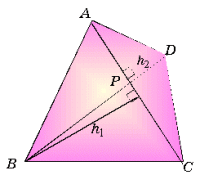ここで四角形ABCDの対角線の交点をPとし、頂点B,Dから対角線ACにおろした垂線の長さをそれぞれ h1,h2 とすれば、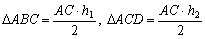
であることより、
△ABC:△ACD=h1:h2=BP:PD
である。よって、BP：PD=t：1-t とおくと、
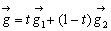
と表される。また、
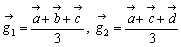
であるから代入して、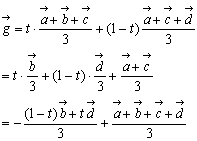
・・・(*)ここで対角線の交点 の位置ベクトルは、BP：PD=t：1-tより
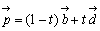
である。また、四角形の物理的重心を
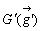とすると、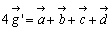
であることより、以上これらの式から、
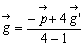
が得られる。
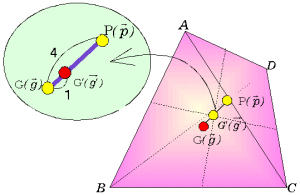
これから四角形の幾何的重心は、四角形の対角線の交点Pと四角形の物理的重心 G' を結ぶ線分 PG' を４：１の比に外分する点であることがわかる。
また、(＊)の式は、対角線BDを(1-t)：tの比に内分する点を
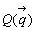とするとき、
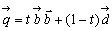より、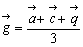
であるから、三角形ACQの重心が四角形の幾何的重心であることを意味している。
これから、四角形ABCDの重心の作図法のひとつとして、対角線BD上にBP>PDであれば、BQ=DPとなる点Qをとり、三角形ACQの重心を求める方法が得られたことになる。