丂丂丂
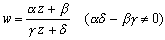
偱偁傞揰w偼丄怴偨側暋慺悢暯柺W傪梡堄偟丄
丂丂丂f : Z 仺丂W
側傞幨憸(懡偔偼Z=W偲側傞偑)傪峫偊傞偨偲偒偺憸偲峫偊傞偙偲偑偱偒傞丅
丂偙偺f偵傛傞憸w傪堦師暘悢娭悢偁傞偄偼(暋慺)堦師曄姺偲偄偆丅偙偺堦師曄姺偼學悢峴楍
丂丂丂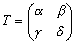
偑惓懃偱偁傞偲偒偵懚嵼偡傞丅偙偙偱丄
丂丂丂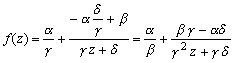
側傞暘夝偑壜擻偱偁傞偙偲偐傜丄堦師曄姺偼師偺俁偮偺曄姺偺崌惉偲傒傞偙偲偑偱偒傞丅
丂丂丂嘆丂f1 : z丂仺丂兛z
丂丂丂嘇丂f2 : z丂仺丂z+兝
丂丂丂嘊丂f3 : z丂仺丂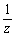
丂偙偺俁偮偺曄姺偑丄嶌梡慺偲偟偰恾宍偵梌偊傞惈幙偵偮偄偰埲壓挷傋偰傒傛偆丅
 仜憡帡(怢弅)偲夞揮曄姺
仜憡帡(怢弅)偲夞揮曄姺
| f1 : z丂仺丂兛z |
丂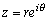 丆
丆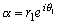 偲偡傞偲丄
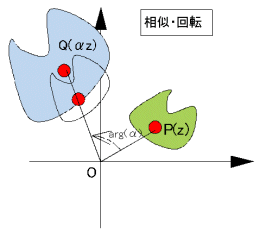
偲偡傞偲丄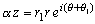 偱偁傞偐傜丄暋慺悢兛偼丄揰P(z)傪尨揰偺夞傝偵兤1夞揮偝偣丄偝傜偵尨揰偐傜偺嫍棧傪r1攞偡傞嶌梡慺偱偁傞丅
偱偁傞偐傜丄暋慺悢兛偼丄揰P(z)傪尨揰偺夞傝偵兤1夞揮偝偣丄偝傜偵尨揰偐傜偺嫍棧傪r1攞偡傞嶌梡慺偱偁傞丅
丂偟偨偑偭偰丄f1偼尨揰傪拞怱偲偡傞怢弅丄夞揮傪昞偡堦師曄姺偱偁傞丅
 仜暯峴堏摦曄姺
仜暯峴堏摦曄姺
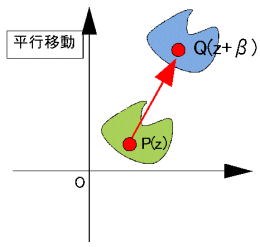
| f2 : z丂仺丂z+兝 |
丂z=x+yi丆兝=u+vi 偲偡傞偲丄z+兝=(x+u)+(y+v)i 傛傝丄w偼z傪幚幉曽岦偵u丄嫊幉曽岦偵v偩偗抣傪憹尭偟偨揰偱偁傞丅
丂偡側傢偪丄f2偼暯峴堏摦(儀僋僩儖検偲傒偰)傪昞偡堦師曄姺偱偁傞丅
|
ex) P(z)偑揰1+i傪拞怱偲偡傞敿宎1偺墌廃忋傪摦偔偲偒丄 丂丂丂丂w=2iz+3-2i 丂傪枮偨偡揰Q(w)偺婳愓傪媮傔傛丅 |
夝)丂2i偺戝偒偝偼2丆曃妏偼90亱傛傝丄2iz偼丄拞怱-2+2i敿宎2偺墌偱偁傞丅
丂丂偙偺墌傪3-2i暯峴堏摦偡傞偲丄
丂丂w偼丄拞怱1 敿宎2偺墌廃忋偺揰偱偁傞丅
 仜憡帡丒幚幉懳徧曄姺
仜憡帡丒幚幉懳徧曄姺
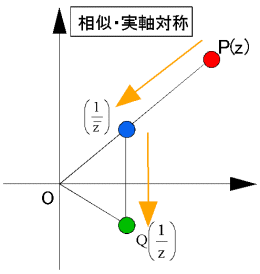
f3 : z丂仺丂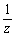
|
丂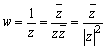 偱偁傞偐傜丄f3偼揰P(z)偵懳偟偰丄OP傪
偱偁傞偐傜丄f3偼揰P(z)偵懳偟偰丄OP傪 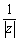 攞偟偰丄偝傜偵幚幉偵娭偟偰懳徧堏摦偟偨曄姺偱偁傞丅
攞偟偰丄偝傜偵幚幉偵娭偟偰懳徧堏摦偟偨曄姺偱偁傞丅
丂偡側傢偪丄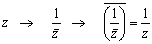 偲側傞丅
偲側傞丅
丂埲忋丄堦師曄姺傪昞偡俁偮偺曄姺偵偮偄偰傒偰偒偨偑丄偦偺偦傟偧傟偼偝傜偵俀偮偺曄姺偵暘夝偱偒傞偙偲偑暘偐傞偩傠偆丅
丂嘆f1 偼夞揮+怢弅
丂嘇f2 偼幚幉曽岦堏摦+嫊幉曽岦堏摦
丂嘊f3 偼怢弅+幚幉懳張堏摦
偱偁傞丅偙偺拞偱丄嘊偺怢弅曄姺偼懠偺曄姺偲戝偒偔堎側偭偰偄傞(傕偪傠傫嘆偺怢弅曄姺偲傕)丅偦傟偼懠偺曄姺偑丄揰P(z)偵懠偺暋慺嶌梡慺傪巤偟偨傕偺偱偁傞偺偵懳偟丄揰嘊偼偦傟帺恎偑嶌梡慺偱偁傞偨傔偵偦傟偧傟偺揰偺怢弅棪偑撈棫偟偰偄傞偙偲偱偁傞丅偦傟偑偙偺曄姺偺恾揑僀儊乕僕偺忈奞偲側傞丅
丂師偵偙偺怢弅曄姺傪弶摍婔壗偺乽斀揮乿偺峫偊曽偐傜暘愅偟偰傒傛偆丅