 f3 : z →
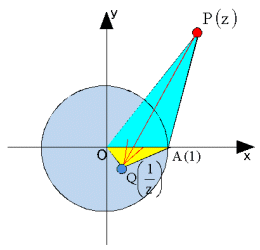
f3 : z → 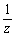 である変換を図示すると右図のようになる。
である変換を図示すると右図のようになる。実際、単位円周上の点A(1)を利用して、⊿OPAと相似であるように⊿OAQを作ると、
OP:OA=OA:OQ
∴ OP・OQ=OA2=1
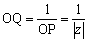
また、arg(z)=θのとき、arg(w)=-θであるから、この点Q(w)が一次変換f3の点P(z)の像を表していることがわかる。
しかし、この図では、伸縮+実軸対称という変換f3のモーションがみえてこない。さらに、作図も困難である。
そこで、伸縮を表す変換である
g : z → 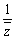
の変換のイメージを図形的に解釈してみよう。
|
原点Oを中心とする半径rの円をCとする。円Cの円外の点Pからこの円に引いた接線の接点をTとし、点Tから線分OPに引いた垂線の足をQとすると、 OP・OQ=r2 である。 |
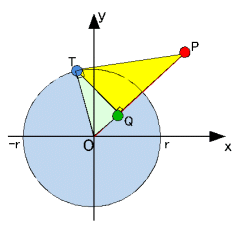 証明)
証明)
PO:OT=OT:OQ
OP・OQ=OT2=r2
このとき、初等幾何では、点Pと点Qは円Cに関して互いに反転(反形あるいは対称)であるという。
また、点Qを中心に考えれば、上述の逆操作から点Pが求められるが、この点Pもまた点Qの反転となる。
すなわち、反転とは、円の内部の点を外部に、外部の点を内部に移す(反転させる)変換である。この反転された点をもとの点の鏡像という。
ここでr=1のとき、OP・OQ=1 すなわち、
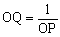
以上より、変換gは、中心原点、半径1の円(単位円)に関する点P(z)の反転変換である。