べき乗変換のイメージ化北海道札幌新川高等学校 中村 文則
０．はじめに
f：z → 1/z なる変換は複素数平面上の広義の円を、広義の円に移すことが初等幾何の反転を利用することで示される。このことは、稲北高校の早苗先生が、レポート「1/z変換をイメージ化する」の中で、関数表示ソフト「Grapes」使って鮮やかにその無限の神秘性を視覚化した。レポートの中盤で氏は、メービウス変換による円の像から一歩進んで、基底である座標平面全体がどう変換されるか試みている。平面を実軸および虚軸に平行な格子に分割して変換したわけである。私の前回のレポート「メービウスのわだち」は、思考で思い描ける範囲のイメージを図式化したものであるが、複素数平面のように複雑なアラベスクを編む曲線ではやはり限界がある。そこで、今回は、Windows上でJIS Full BASICの環境を実現することを目標に作成された言語処理システムである十進ＢＡＳＩＣ(文教大学教育学部 白石和夫氏)および、関数描画ソフト「Grapes」(大阪教育大学附属高等学校 友田勝久氏)を使って複素数平面の神秘性について触れて見ようと思う。特に、
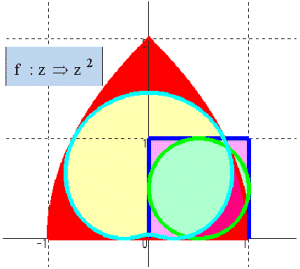
f : z → zp (p∈Q) なるベキ変換による
① 半径１の円の変換 ②座標平面全体の変換
について調べてみよう。