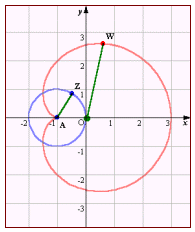
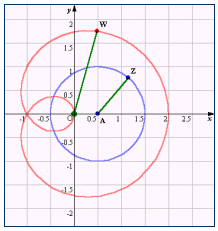
 z=r(cosθ+sinθ)とすれば、|w|=r2,arg w=2θ である。zが中心Oで半径1の円であれば、wも中心O、半径1の単位円であることは容易に予想されよう。では半径1の円を実軸、虚軸の方向に平行移動した円の像はどうなるか調べてみよう。
z=r(cosθ+sinθ)とすれば、|w|=r2,arg w=2θ である。zが中心Oで半径1の円であれば、wも中心O、半径1の単位円であることは容易に予想されよう。では半径1の円を実軸、虚軸の方向に平行移動した円の像はどうなるか調べてみよう。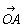 ,
, と同一視できる。
と同一視できる。 とすると、これから、
とすると、これから、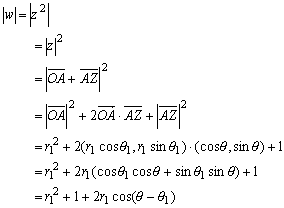
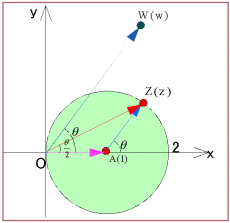
 ここで、r=|w|とすると、極方程式
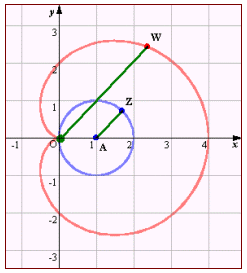
ここで、r=|w|とすると、極方程式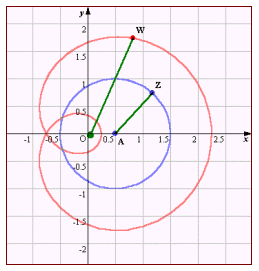 では、A(1/2) とするとどうなるだろうか。
では、A(1/2) とするとどうなるだろうか。 このように、wの偏角が曲線カージオイドを加工して様子が分かるがそれを式として表現することは難しい。そこで、arg w=ψ(θ) として、
このように、wの偏角が曲線カージオイドを加工して様子が分かるがそれを式として表現することは難しい。そこで、arg w=ψ(θ) として、
なお、このことは、中心が実軸上にある点のみならず、複素数平面上のすべての点についていえることである。
|
ex) |z|=1であるとき、次の複素数wの軌跡を求めよ。 (1) w=z2-2z (2) w=z2+z |

