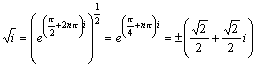2. w=√z の像
複素数における根号の定義は実数の場合と同様に考えることができるが、根号は2つの値を意味する。
√z=±(a+bi) である。例えば、
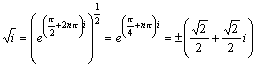
である。したがって w2=z のグラフを考えればよいことになる。
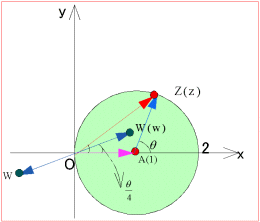 w4=z2 であるから、
w4=z2 であるから、
|w4|=r12+1+2r1cos(θ-θ1)
である。ここで、A(1)とすると、
|w4|=2(1+cosθ)=4cos2θ/2
よって、 |w2|=2cosθ/2
となる。また、arg Z=±π/4 である。
したがって、
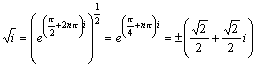
である。
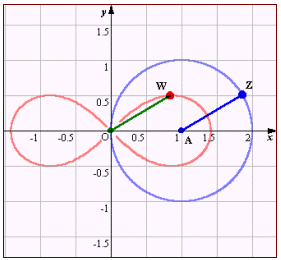
この曲線を連珠形(lemniscate)という。レムニスケートは2点-1,1からの距離の積が等しい点の軌跡を表すが、これは、負の実数の範囲で描かれる曲線と、正の実数の範囲で描かれる曲線を連結した形になっている。ここで、Aの値を実軸上で変化させると下図のような曲線が描かれる。
この図から、円zの中心A(α)は、連結している2つの閉曲線のくっつきの度合いを示していることが予想できる。以下、性質をまとめると、
- グラフは原点に対して対称である。
- |z|<1 のときは、2つの閉曲線は他方の閉曲線に割りこみ、楕円のような形をつくる。
|z|=1 のときは、2閉曲線は接し、レムニスケートとなる。
|z|=1 のときは、2閉曲線は接し、レムニスケートとなる。
|z|>1 のときは、2閉曲線は離れていく。
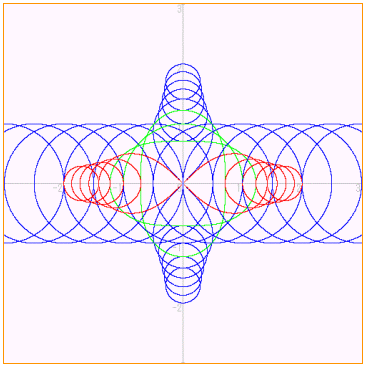
《描画例》……十進BASICによる描画
下図は、半径1の円の中心A(α)を変えたときの w=√z のグラフである。シャボン玉を引き離したらプチッと切れて2つのシャボン玉になったような印象を与える。
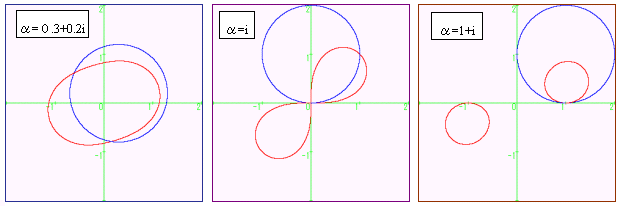


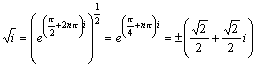
 w4=z2 であるから、
w4=z2 であるから、