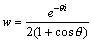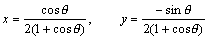3. w=1/z2 の像
f:z2 → 1/z2 であるから、この変換は、z2に関するメービウス変換である。
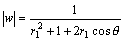 となるがこれから曲線の外形を予想することは難しい。ただ、r1=1 すなわち、中心1半径1の円の場合は、
となるがこれから曲線の外形を予想することは難しい。ただ、r1=1 すなわち、中心1半径1の円の場合は、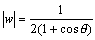 であり、arg w=-θであるから、
であり、arg w=-θであるから、
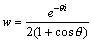
となる。ここで、w=x+yi とすると
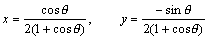
となり、これは、放物線を表すことが分かる。一般に極方程式では、

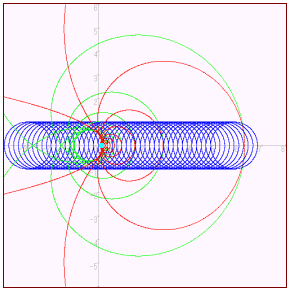
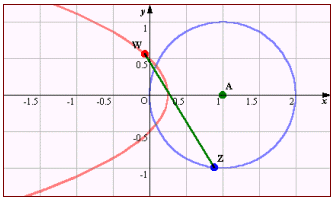
は2次曲線を表すが、メービウス変換は、原点に近いものをより遠ざけ、遠いものは近づけるから、|w|から得られる極方程式の影響はほとんど考えられない。実際、描画をしてみると下図のようになる。BASICの実行から予測すると、半径1、中心A(α)の円に対して、αを実軸上にとり、-∞<α<∞ で変化させると、
カージオイド ⇒ エピサイクロイド ⇒ 放物線 ⇒ カージオイド ⇒ 原点
と変化していく。


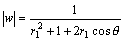 となるがこれから曲線の外形を予想することは難しい。ただ、r1=1 すなわち、中心1半径1の円の場合は、
となるがこれから曲線の外形を予想することは難しい。ただ、r1=1 すなわち、中心1半径1の円の場合は、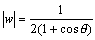 であり、arg w=-θであるから、
であり、arg w=-θであるから、