Ⅱ.座標全体の変換
べき乗変換により座標平面全体はどう変換されるか考えてみよう。
f:Z → W なる変換において、ZとWを同じ複素数平面とし、実軸および虚軸に平行な直線(座標の格子)を変換してみる。
1.f(Z)=1/z の像
 メービウス変換の性質として、原点を通らない直線は原点を通る直線に変換されることは既知のことである。反転の考え方から原点に近い点は原点から遠ざかり、原点から離れた点は原点に近づく。直線の場合は、-∞と∞の点はともに原点に収束し、ジョイントされ円になるわけである。直線を半径が無限大の円と広義にみて、これを円々対応という。
メービウス変換の性質として、原点を通らない直線は原点を通る直線に変換されることは既知のことである。反転の考え方から原点に近い点は原点から遠ざかり、原点から離れた点は原点に近づく。直線の場合は、-∞と∞の点はともに原点に収束し、ジョイントされ円になるわけである。直線を半径が無限大の円と広義にみて、これを円々対応という。
よって、実軸に平行な原点を通らない直線(すなわち実軸以外)は、原点を通る円に変換される。直線がもっとも原点に近づく点、すなわち原点から直線におろした垂線の足(虚軸上の点である)を共役反転の性質から実軸に対称移動した点が、直径の他端である。円は、実軸に平行な直線と原点の距離が遠ざかればその半径は小さくなっていく。
また、虚軸に平行な直線も同様なことがいえる(直線は実軸対称であるから共役変換は起こらない)。
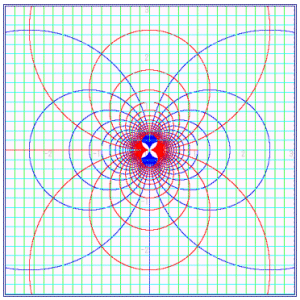
このことを十進BASICで描画し検証したのが、右図である。
実軸に平行な直線が右から左へと点をプロットすると、円は時計回りに描かれ、虚軸に平行な直線が下から上へと点をプロットすると、半時計回りに円が描かれることが分かる。
ところで、メービウス変換は、等角写像の代表例としても知られている。等角とは、二曲線の交角の大きさが変換後も不変であるということであるが、このことは、早苗氏のレポートにも触れられている。
ではメーピウス変換についてその等角写像性を調べてみよう。
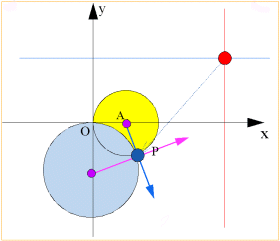 複素数平面の格子を表す直線x=s と直線 y=t のfによる像は反転の考え方から、
複素数平面の格子を表す直線x=s と直線 y=t のfによる像は反転の考え方から、
x=s ⇒ 中心 A(1/2s) 半径 |1/2s|の円
y=t ⇒ 中心 B(-1/2t・i) 半径 |1/2t|の円
である。二直線はもちろん直交し、交点 s+ti の像P(w)は、
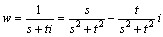
である。
よって、上で求めた2円が直交すればよい。さてここで2曲線が直交することとは、その交点における各曲線の接線が直交するということである。特に円については接線の法線は円の中心を通るから、中心と接点を結ぶ2つの直線が直交すればよいことになる。
すなわち、2円の中心と交点を結ぶベクトル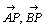 に対して、
に対して、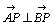 が言えればよい。
が言えればよい。
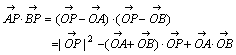
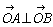 より
より 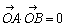 また、
また、
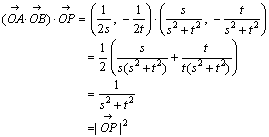
以上より、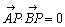 となり、等角写像性が示されたことになる。
となり、等角写像性が示されたことになる。
 複素数平面の格子を表す直線x=s と直線 y=t のfによる像は反転の考え方から、
複素数平面の格子を表す直線x=s と直線 y=t のfによる像は反転の考え方から、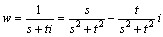
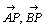 に対して、
に対して、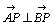 が言えればよい。
が言えればよい。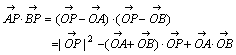
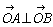 より
より 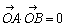 また、
また、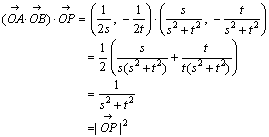
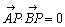 となり、等角写像性が示されたことになる。
となり、等角写像性が示されたことになる。 メービウス変換の性質として、原点を通らない直線は原点を通る直線に変換されることは既知のことである。反転の考え方から原点に近い点は原点から遠ざかり、原点から離れた点は原点に近づく。直線の場合は、-∞と∞の点はともに原点に収束し、ジョイントされ円になるわけである。直線を半径が無限大の円と広義にみて、これを円々対応という。
メービウス変換の性質として、原点を通らない直線は原点を通る直線に変換されることは既知のことである。反転の考え方から原点に近い点は原点から遠ざかり、原点から離れた点は原点に近づく。直線の場合は、-∞と∞の点はともに原点に収束し、ジョイントされ円になるわけである。直線を半径が無限大の円と広義にみて、これを円々対応という。