２．f(Z)=z2 の像
メービウス変換はその特徴的な性質から格子の変換が容易に予測できたが、次にw=z2の変換はその性質も含めて変換を調べていこう。
まず、実軸そのものの変換は、実軸をz=t (ｔ∈Rと表すと、w=t2≧0 となるから実軸の正の部分に変換される。
zが-∞から∞に向って変化すると、その像は+∞から原点に向って動き、原点をおり返してまた無限の彼方に消えていくわけである。
同様に、虚軸は、z=it (ｔ∈R) と表されるから、w=-t2 ≦0である。虚軸上 -∞i から ∞i に向って値が変化すると、実軸上 -∞ から増加し、原点で折り返して負の無限大に消えていく。
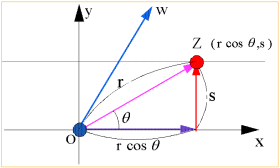
次に、実軸に平行な直線y=sを変換する。このとき直線上の点は、
P(r cosθ，s)
と表すことができる。
また、
cos2θ=cos2θ-sin2θ
=cos2θ-s2/r2
sin2θ=2sinθcosθ
=2s/r・cosθ
であるから、
w=z2
=r2(cos2θ+isin2θ)
=(r2cos2θ-s2)+i2srcosθ
これから像を表す極形式が得られた。
ではこの像はどんな図形になるだろうか。
そこで、w=x+yiとすると、
x=r2cos2θ-s2
y=2srcosθ
２式より を消去して、
x=y2/4s2-s2
整理して p=s2 とおけば、
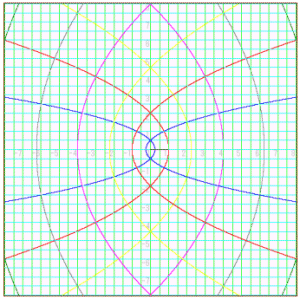
y2=4p(x+p) (p＞0) ………(*)
これは、原点を焦点とする、準線x=-2p の放物線である。
sの値を-∞から∞に向って変化させると、p=s2であるから、準線x=-2pは-∞から原点を折り返してまて戻っていく。したがって放物線の実軸正方向に延びたグラフの開きは、だんだん小さくなりそしてまた開いていくことが分かるだろう。
また、虚軸に平行な直線であるが、これは実軸に平行な直線を90度回転させたものと考えていいから、z=iz1(z1は実軸平行の直線)とおくと、w=z2=-z12 となる。したがって、直線x=sの像は、直線y=sの像を原点対象したものである。
よって、その方程式は、
y2=-4p(x-p) (p＞0)
となり、これもまた焦点が原点の放物線であり、実軸負の方向に延びた開きは点がzの格子上の点が下方から上方に変化するとき、だんだん小さくなり原点で折り返してまた増加していく。
以上よりfによるzの格子の像は、原点を焦点とし、実軸を軸とする放物線の集合(共焦点放物線族) である。
十進ＢＡＳＩＣで描画した図で確認いただきたい。
では次に w=z2 の等角写像性について調べてみよう。
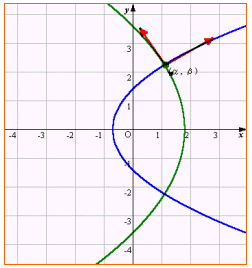
格子点の１つ(s,t)のfによる像を P(x0,y0) とすると、この点を通る１組の放物線が決まってくる。それは、
ψ(p)=4p2+4x0p-y02
とおいたとき、二次方程式 ψ(p)=0 の２解 p=α,β に対応する放物線である。このとき、解と係数の関係より、
αβ=-y02/4
である。２つの放物線の接線の傾きの積を求めると、
2α/y0×2β/y0=4αβ/y02=-1
よって、２つの放物線は直交する。
したがって写像 f(z)=z2 についても等角写像性がいえたことになる。