3.f(Z)=√z の像
まず、実軸上の点z=t (t∈R) であるが、t>0 のときは、実軸の正の部分に移され、t<0のときは、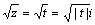 より、虚軸の原点より上の部分に移される。
より、虚軸の原点より上の部分に移される。
また、虚軸上の点 z=ti (t∈R) については、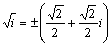 であるから、t>0のとき、
であるから、t>0のとき、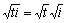 より直線 y=x 上の点に変換される。また、
より直線 y=x 上の点に変換される。また、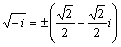 より、t<0のとき、
より、t<0のとき、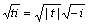 より直線 y=-x 上の点に変換される。
より直線 y=-x 上の点に変換される。
次に、z=reiθ とおくと、
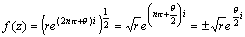
と表される。そこで w=x+yi とおくと、
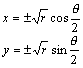
二式を辺々かけて、
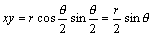
ここで、実軸に平行な直線上の点を (rcosθ,s) とおくと、sinθ=s/r であるから、xy=s/r を得る。
すなわち、その像は、x軸、y軸を漸近線とする直交双曲線である。
s>0 のとき、xy>0 より、第1象限、第3象限に広がる双曲線。s<0のときは、xy<0 より、第2象限、第4象限に広がる双曲線であり、双曲線族の頂点と原点との距離は|s|となる。
次に虚軸に平行な直線については実軸に平行な直線 z1 を -i だけ回転させると、
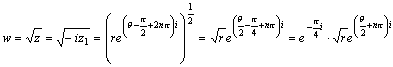
よって、双曲線 を原点の回りに -45°回転させた曲線であることがわかる。
すなわち、その像は、直線 y=±x を漸近線とする双曲線である。
 s>0のときは、実軸を軸とする左右に広がる双曲線
s>0のときは、実軸を軸とする左右に広がる双曲線
x2-y2=s2
であり、s<0のときは、虚軸を軸とする上下に広がる双曲線
y2-x2=s2
である。
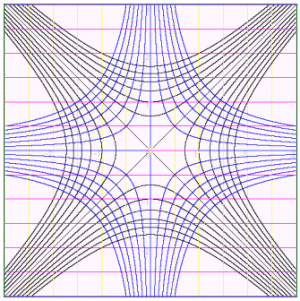
十進BASICで描画すると、シンメトリーな曲線が浮かび上がってくる。
最後に、y=√z の等角写像性について調べよう。
Z平面上の格子点の像である点を変換すると、
双曲線 xy=±s/2 と x2-y2=±s2 の交点 (x0,y0) に移される。それぞれの曲線を微分して交点における接線の傾きを求めよう。
y+xy'=0 より dy/dx=-y0/x0
2x-2yy'=0 より dy/dx=x0/y0
よって二式を辺々掛けると、
-y0/x0・x0/y0=-1
以上より接線どうしが直交する。よって、等角写像性が示された。
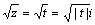 より、虚軸の原点より上の部分に移される。
より、虚軸の原点より上の部分に移される。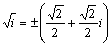 であるから、t>0のとき、
であるから、t>0のとき、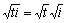 より直線 y=x 上の点に変換される。また、
より直線 y=x 上の点に変換される。また、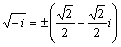 より、t<0のとき、
より、t<0のとき、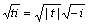 より直線 y=-x 上の点に変換される。
より直線 y=-x 上の点に変換される。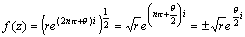
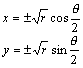
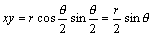
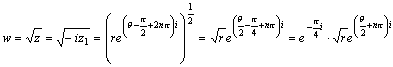
 s>0のときは、実軸を軸とする左右に広がる双曲線
s>0のときは、実軸を軸とする左右に広がる双曲線