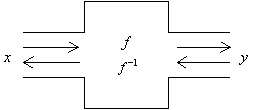
fの操作をするブラック・ボックスの逆の働きについて考えてみよう。これはこのブラック・ボックスの入力と出力を逆転して考えればよいことになる。普通の装置では一般に可逆ではないが，思考の上では逆転して考えることができる。入力xがfの働きにより出力y=f(x)となるとき，このyが出力となり，fと逆の働き
f−1の働きを受けて，出力はx=f−1(y)となる。この働きf−1をfの逆関数と呼んでいる。つまりf(x)=yが成り立つときx=f−1(y)となる。
2次関数は変化率が一定でない関数の中でごく身近なものとして代表的な例といえる。この関数の変化の様子を調べる為にグラフを書くと放物線と呼ばれる曲線となり，最大･最小，頂点等を求め，更に方程式・不等式を解いてゆく際の補助手段として利用されたりする。2次関数のグラフの概形は一般形としてのy=ax2+bx+cを標準形y=a(x−p)2+qへと変形してイメージされる。この為，平方完成の計算に全力をあげることになるが，一般形の段階でグラフの概形がわかっていた方が内容は把握し易く，計算にも見通しを立て易い。一般形における2次式の係数a，b，cの意味については，aはグラフの開き，cはy切片，bは軸に関係しているという捉え方が定着している。このbの性格については別な捉えかたもあり，むしろその方がグラフをイメージし易くなることに着目したのが"和関数"という考え方である。
2つの関数y=g(x)，y=h(x)に対して，y=g(x)＋h(x)をg(x)，h(x)の和関数といい，そのグラフはg(x)，h(x)のどちらかのグラフを基準にして，その上にもう一つの関数の値を加えてゆけばよい。f(x)=ax2＋bx＋cをg(x)=ax2とh(x)=bx+cの和関数とみると，直線上に2次関数の基本形の値を加えてゆけばよい。そして，x=0のときf(x)とh(x)は共有点をもつ。しかもh(x)はx=0におけるf(x)の接線となる。このことからf(x)=ax2＋bx＋cのグラフは直線h(x)=bx+cを描き，グラフの開きがaである放物線をx=0で接するようにh(x)の上に乗せる（或は下にぶらさげる）とよい。このプランは札幌新川高校・中村先生によって提案実践されている。また札幌藻岩高校・菅原先生からは，2次関数の切片形からの導入・展開が試みられている。これからも色々な工夫・実践の報告が期待されるところである。現在関数教材は各学年に分断された形で展開されており，関数一般という概念をまとめきれない事情に置かれている。この為，個々の2次関数とか三角関数とか，分数関数等のグラフの性質等に意識が向けられてゆく。微積分の概念を深めていこうとするとき関数の概念がきちんと把握されていなければならない。また図形の対応や，領域の対応を考えたりする場合も根底には関数としての対応の概念がよく理解されていることが必要である。もともと関数とはきわめて広い内容をもった概念であり，それは対応，写像，変換，操作という名でおきかえ得る豊富な内容を持っている。まず現代では関数とはどのように定義されているのかを見てみよう。
"関数"2つの集合M，Nがあって，Mの任意の元xに対してNの1つの元yが確定するとき，このxからyへの対応の規則fをMからNへの写像，あるいは関数といって，f；x∈M→y=f(x)∈N，あるいはf；M→Nと表す。このときMを関数fの定義域，Nをfの値域をいう。またxを独立変数（自変数），yを従属変数という。
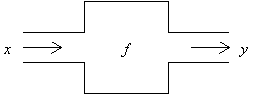この定義において注目すべきことは，関数の本質は集合から集合への対応，或は変数から変数への対応であり，従って対応の規則に目を向けているという事と，xやyは自変数，従変数としてfとは独自な概念として規定されていることである。またx，yにあてはまるものは数でなくても，数の組，ベクトル，点の座標，その他何らかの集合の元であればよい。そこで最初に"関数とは何か"を述べるときに関数のさまざまな意味の拡張に適応できるような形でまとめておくことが望ましい。関数fのもつ働きや，対応のさせ方が容易に思い浮かべられるようなシェーマを工夫することが必要である。このようなシェーマとして適当と考えられるのがブラック・ボックス（暗箱）である。ブラック・ボックスとは内部のからくりがどうなっているかは別問題として，とにかく何らかの仕掛けによって一定の操作を行う装置である。入ってくるもの（入力）に加工を施したもの（出力）を外部に送り出す働きを持っている。次の図は入力xがfの操作を受けて加工されてyになり，それが出力として出てきたことを意味している。これを式ではf(x)=yと表わす。f(x)の（ ）は入力の入口と考えることができて，この入口から入力xが入ってゆき，fの操作を受けてf(x)となりそれが出力yなのであると考えるとよい。入力xに対して或る作用を加えて出力yとして対応させる対応のさせ方がブラック・ボックスの働きfとして表わされているのである。次にfの働きをするブラック・ボックスとgの働きをするブラック・ボックスを直列につないで考えることにより合成関数g○fやf○gについて考えることができる。また並列につなぐことにより関数の和f+gについて考えることができる。（別冊資料レポート参照）
fの操作をするブラック・ボックスの逆の働きについて考えてみよう。これはこのブラック・ボックスの入力と出力を逆転して考えればよいことになる。普通の装置では一般に可逆ではないが，思考の上では逆転して考えることができる。入力xがfの働きにより出力y=f(x)となるとき，このyが出力となり，fと逆の働き
f−1の働きを受けて，出力はx=f−1(y)となる。この働きf−1をfの逆関数と呼んでいる。つまりf(x)=yが成り立つときx=f−1(y)となる。
y=f(x)=3x+5について考えてみよう。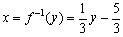
，文字にとらわれずにfとf−1の働きの違いは次のように書いたほうがわかりやすい。
fの方はf( )=3( )+5でf−1の方は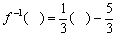
となる。( )の中にどんな文字が入っているか，xかyであるか等ということは本質的なことではない。しかし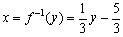，とした上で自変数はxで，従変数はyでf−1の働きを表わすとすれば
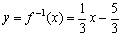となる。このときy=f(x)のグラフとy=f−1(x)のグラフは直線y=xに関して対称となる。
では定数関数y=f(x)=π（x∈R）について考えてみよう。f(1)=π，f(2)=π，・・・となるがy=πに対応する入力としてのxは特定できない。この場合はf−1は存在しない。従って逆関数が与えられるのはfが1対1の対応である場合のみであることがわかる。以上述べてきたことはすべてシェーマとしてブラック・ボックスをえがくことにより明確に把握することができる。かつて"関数"は"函数"と表記されてきた。functionが漢訳される際に発音が似ている函の字をあて，数学に関する用語として"函数"としたのではないかという話を何かの本で読んだ事がある。実に名訳だなと思うと共に，ブラック・ボックスこそ本当の意味での"函数"なのではないかとつくづく思うのである。