【2】複素数の不思議
2次関数y=x2−4x+7のグラフは頂点が(2,3)の放物線となる。このグラフとx軸には共有点がない。2次方程式x2−4x+7=0は虚数解を持ちx=2±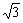 iとなる。この解の実部,虚部の2,
iとなる。この解の実部,虚部の2,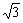 と頂点(2,3)の間には深い関係がある筈だが,それはグラフの上ではどのような形で現れているであろうか。このような疑問を高校生の頃に感じた人は多いのではなかろうか。私がこの疑問に対してある程度の納得できる解決を得たのは高校・大学を経て,高校の数学教師となってからかなりの年月を経過してからであった。"現代数学"という雑誌に或る数学者の書いたもので,y=f(x)のグラフにおいてx=u+viとおく。このときyをA+Biの形で表わし,yが実数になる場合をu軸,v軸,y軸とによる一種の空間座標によって視覚化させるといったものであった。この記事の中では2次方程式の虚数解,3次方程式の虚数解についてかなり詳細に論じられていたという記憶がある。
と頂点(2,3)の間には深い関係がある筈だが,それはグラフの上ではどのような形で現れているであろうか。このような疑問を高校生の頃に感じた人は多いのではなかろうか。私がこの疑問に対してある程度の納得できる解決を得たのは高校・大学を経て,高校の数学教師となってからかなりの年月を経過してからであった。"現代数学"という雑誌に或る数学者の書いたもので,y=f(x)のグラフにおいてx=u+viとおく。このときyをA+Biの形で表わし,yが実数になる場合をu軸,v軸,y軸とによる一種の空間座標によって視覚化させるといったものであった。この記事の中では2次方程式の虚数解,3次方程式の虚数解についてかなり詳細に論じられていたという記憶がある。
また,「話題源数学」の中にも,虚数解のイメージ化ということで簡単に触れられている。上の問題について考えてみよう。
y=x2-4x+7においてx=u+viとおく。(u,vは実数)
y=(u+vi)2−4(u+vi)+7=u2−4u+7−v2+2v(u−2)i
となりReal y=u2−4u+7−v2となる。x=u+viはu,vを両座標軸にとった平面(複素平面)上の点(u,v)で表わされ,この平面に対して,原点より垂直に実数軸を立てた空間を考えこの3次元空間でy=f(x)=f(u,v)の図形を考えてゆくことになる。Real yの示す図形は一般に複雑な曲面となる。yが実数となるのはv=0とu=2の場合でそれぞれについて考えてみよう。
- v=0,Real y=u2−4u+7−v2は曲面y=u2−4u+7−v2と平面v=0との交線で,uy平面(xy平面)における放物線となる
- u=2,Real y=u2−4u+7−v2は曲面y=u2−4u+7−v2と平面u=2との交線で,平面u=2の上でvy軸をもとにした放物線となり,y=3−v2となる。y=0となるのはv=±
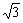 で,これはuv平面との交点が(2,±
で,これはuv平面との交点が(2,±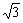 )となることを意味し,x=2±
)となることを意味し,x=2±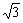 iとなる。
,y=3−v2となる。y=0となるのはv=±
iとなる。
,y=3−v2となる。y=0となるのはv=±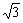 で,これはuv平面との交点が(2,±
で,これはuv平面との交点が(2,±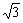 )となることを意味し,x=2±
)となることを意味し,x=2±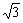 iとなる。
iとなる。
以上少し調べてみたように虚数解を視覚化するのは意外に難しい。複雑な曲面を考え,更にそれをある平面で切ったときの切り口に現れる図形について考えるといったような困難がつきまとう。コンピュータグラフィックスの理論,技術が開発され,立体図形を画像化することが可能となってきた。複雑な曲面もコンピュータによる画像を観察しつつ考えてゆけば比較的容易に考えを進めてゆくことができる。札幌稲北高校・早苗先生の"虚数解のイメージ化""虚円のイメージ化"はこのことを示している。(別冊資料参照)
「2円x2+y2−6x−8y+14=0とx2+y2−4=0は交わらないが,2円を引いて得られる直線3x+4y=24は何を意味するか」。私共の研究会での夏季セミナーの後の懇親会で数学談義に花を咲かせている中でこのことが話題にあがった。三年前のことである。当時は,たぶんこの直線は「虚円」に関係しているのではないかということでお互いに調べてみよういうことで終わった。その後札幌新川高校・中村先生がこの問題を追求し,根軸,方べきの定理に深い関わりを持っていることが明らかにされた。しかし,複素数平面との関連で虚円とどのような関連があるかについては更に追求していかなくてはならないことが論議された。そして早苗先生のコンピュータ・グラフィックスによるアプローチが大きな手助けとなり,中村先生の"Shadow Line 〜その存在性をめぐって〜"によって一応の解決を得たのである。(このレポートは日数教山口大会で発表された。)
このように従来はグラフの上に現れてこない複素数にまつわる不思議さが,複素数平面と実数軸を組み合わせた一種の3次元空間を考え,その中で曲面や平面の関連として視覚化されるようになってきた。このような道がひらかれてきたのも,複素数平面が導入されることによって可能となったといってよいであろう。
しかし,複素数についての教育上の問題点がこれで解決したとは言えないであろう。複素数とは何かについての根本的な疑問点,複素数の計算法は何故あのような考えでよいのか等については教育現場における取り扱いは相当にあいまいなものをかかえたままで経過してきていると思われる。
ここで田村二郎先生が,その著書"量と数の理論"の中で述べられている一部分を引用してみよう。
「複素数とは何か。伝統的な学校の数学は,昔も今もこの問に答えない。学校で学ぶのは複素数の計算法だけである。ともかくも,複素数はa+bi…(1)という形に書かれる。複素数(1)の意味を明らかにするためには,次の三つの問に答えなければならない。
- 虚数単位iは条件i2=−1を満たす。このような数iとは何か。
- bとiの積は何か。
- aとbiの和とは何か。」
また,この本のはしがきの中で次のように述べておられる。やや長くなるが引用してみよう。
「従来,数の理論を厳密に展開するときには,たいてい素材を"自然数"に限定し,量の概念を介入させない方法がとられてきた。この型の理論を学ぶ道はすでに開かれており,われわれはすぐれた書物によって,純粋数学の美しさを十分に味わうことができる。しかしながら,経験に基づく諸科学が数学と交錯するところでは,量と数のあいだにある密接な関係を無視することができない。この場合,量はもちろん経験科学に属する概念である。それでもなお"確からしさの数学""空間の数学""ポテンシャルの数学"などが成り立つように,量の基本性質にもとづく数学の理論を展開することは可能である。―――,もともと異質の概念である量と数を明確に区別し,数を量空間の変換とみなす。―――この考え方は決して新しいものではない。とりわけ,1944年に公表された南雲道夫先生の理論は,ユークリッド式・量と正の実数との関係を簡潔明快に説いて余すところがない。私が南雲先生の理論に付け加えたものがあるとすれば,対称性をもつ量空間,すなわち有向量からなる空間の概念だけであろう。この量空間の変換として負の数を導入すれば,スタンダール以来学習者を悩ませてきた"正負の数の計算法則"は一つの定理として簡単に証明される。また,複素数を平面有向量の変換の中に見いだすのも容易であろう。」
複素数概念の明解な理解の仕方,またそれを教育現場で具体化しようと志すとき,上記の田村理論の検討は避けて通ることのできない課題であると思われる。(別冊資料参照)
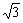 iとなる。この解の実部,虚部の2,
iとなる。この解の実部,虚部の2,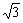 と頂点(2,3)の間には深い関係がある筈だが,それはグラフの上ではどのような形で現れているであろうか。このような疑問を高校生の頃に感じた人は多いのではなかろうか。私がこの疑問に対してある程度の納得できる解決を得たのは高校・大学を経て,高校の数学教師となってからかなりの年月を経過してからであった。"現代数学"という雑誌に或る数学者の書いたもので,y=f(x)のグラフにおいてx=u+viとおく。このときyをA+Biの形で表わし,yが実数になる場合をu軸,v軸,y軸とによる一種の空間座標によって視覚化させるといったものであった。この記事の中では2次方程式の虚数解,3次方程式の虚数解についてかなり詳細に論じられていたという記憶がある。
と頂点(2,3)の間には深い関係がある筈だが,それはグラフの上ではどのような形で現れているであろうか。このような疑問を高校生の頃に感じた人は多いのではなかろうか。私がこの疑問に対してある程度の納得できる解決を得たのは高校・大学を経て,高校の数学教師となってからかなりの年月を経過してからであった。"現代数学"という雑誌に或る数学者の書いたもので,y=f(x)のグラフにおいてx=u+viとおく。このときyをA+Biの形で表わし,yが実数になる場合をu軸,v軸,y軸とによる一種の空間座標によって視覚化させるといったものであった。この記事の中では2次方程式の虚数解,3次方程式の虚数解についてかなり詳細に論じられていたという記憶がある。