xyz空間において,x軸と平行な柱面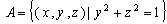 からy軸と平行な柱面 からy軸と平行な柱面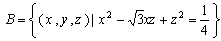 により囲まれる部分を切り抜いた残りの図形をCとする。図形Cの展開図を描け。ただし,点(0,1,0)を通りx軸と平行な直線に沿ってCを切り開くものとする。 により囲まれる部分を切り抜いた残りの図形をCとする。図形Cの展開図を描け。ただし,点(0,1,0)を通りx軸と平行な直線に沿ってCを切り開くものとする。
|
関数概念の説明にブラックボックスを利用し効果をあげている教師達がいる。しかもそのブラックボックスは手作り教具である。また空間図形や平面図形に親しむために"折り紙"を積極的に活用している教師達もいる。最近注目されている"オリガミクス"という語が出来ていない頃から地道な工夫が続けられている。定規とコンパスを使う幾何学とは違って,折り紙では1カ所折ると紙が一緒についてくるのでいくつかの点と線が同時に決まる。従って,より複雑な幾何学的処理ができるのだという。正確な寸法が必要な正多角形,正多面体,複合多面体など,通常では作りにくい教材が折り紙では容易にできてしまう。折り紙の多面体を部品に使って,結晶構造や分子構造を作ることもでき化学の講義にも利用されているという。アンテナや太陽電池のように,はじめはコンパクトにたたんでおいて宇宙空間で大きく広げる必要があるものに対して宇宙科学研究所の三浦公亮博士が科学折り紙の方法を提案し応用されているという。またフラクタルでさえも折り紙で再現できるのだという。岩見沢緑陵高校の加藤先生は長年"折り紙の数学"を研究してこられた道内の権威であるが,次のように述べておられる。
「多面体の作製に取り組んでから,立体の展開図が頭に浮かぶようになりました。手を使うということが大事なことだと思います。折り紙の意義も楽しさだけでなく,そんなところにあるのではないか。子供の時にこのような体験を豊富にもっておくことが,空間概念の形成につながってゆくのではないでしょうか。」(別冊資料参照)
折り紙は曲線の理論には不向きと考えられてきたが,包絡線の理論を使うと2次曲線に折り紙を利用することも可能であるという。小樽桜陽高校 岡部先生が前任校で行った研究授業は"直線で何が描けるか"というテーマのもとに,このことを実証するものであった。まさに先見の明というべきものであろう。
(別冊資料参照)
空間図形は図に書きにくいことから何となく敬遠され難解なものと思われがちである。例えば(92東京大・理系)の或る問題を見てみよう。
xyz空間において,x軸と平行な柱面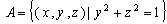 からy軸と平行な柱面 からy軸と平行な柱面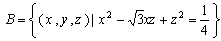 により囲まれる部分を切り抜いた残りの図形をCとする。図形Cの展開図を描け。ただし,点(0,1,0)を通りx軸と平行な直線に沿ってCを切り開くものとする。 により囲まれる部分を切り抜いた残りの図形をCとする。図形Cの展開図を描け。ただし,点(0,1,0)を通りx軸と平行な直線に沿ってCを切り開くものとする。
|
 この問題は,ペットボトルを利用した手作り教具によって分かり易く説明することができるという。根室高校の長谷川先生は他にも解法のイメージ化が浮かびにくい問題について手作り教具による分かり易い工夫をしておられる。(別冊資料参照)
この問題は,ペットボトルを利用した手作り教具によって分かり易く説明することができるという。根室高校の長谷川先生は他にも解法のイメージ化が浮かびにくい問題について手作り教具による分かり易い工夫をしておられる。(別冊資料参照)
模造紙が示す最大値・最小値。0≦x≦2 における関数 f (x)=−x2+2axの最大値・最小値を求めよ。この種の問題はグラフを何回も板書したり,また説明にも苦労するものであるが模造紙を使ってうまく説明できるという。札幌稲雲高校の大河内先生は実践後次のように述べておられる。
"実際に模造紙を丸めたり,切ったりしている最中は「何が始まるのだろうか」と興味津々の様子でこちらの出方をうかがっていた。また,実際に模造紙を使って説明を始めると歓声が上がり「こんな事でこんなにうけるものならもっと早くやれば良かった」とこちらが逆に驚かされるような反応が返ってきた。生徒からは,「どうして授業の時にやってくれなかったんですか」とか「授業でわからなかったことが今回はよくわかりました。」という声を聞かせてもらい,まずまずの手応えを得た"(別冊資料参照)手作り教具の工夫には秘められた威力を感ずる。これからも多くの工夫を集積し,効果的な指導法,説明法に役立てたいものである。