確率の導入段階でサイコロが例としてよくとりあげられている。それぞれの面の出る確率はいずれも
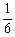 である等と説明される。そしてこの時,理想的にできているサイコロならば…とか,何らのくせもなく作られたサイコロならば…等というただし書きが付け加えられる。
である等と説明される。そしてこの時,理想的にできているサイコロならば…とか,何らのくせもなく作られたサイコロならば…等というただし書きが付け加えられる。
確率の導入段階でサイコロが例としてよくとりあげられている。それぞれの面の出る確率はいずれも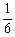 である等と説明される。そしてこの時,理想的にできているサイコロならば…とか,何らのくせもなく作られたサイコロならば…等というただし書きが付け加えられる。
である等と説明される。そしてこの時,理想的にできているサイコロならば…とか,何らのくせもなく作られたサイコロならば…等というただし書きが付け加えられる。
しかし,よく考えてみれば理想的にできているサイコロにしても,何らのくせのないサイコロにしても,現在の技術水準をもってしても作り得ないものであろう。それなのに我々は何となく,6つの面の出る確率が等しいサイコロが本来存在して,現実のサイコロはそれに比べて出来の悪いサイコロなのだという受け取り方をすることが多いのではないだろうか。ここまでくると"何らくせのないサイコロ"とは"仮想モデル"と呼ぶのがふさわしいのではないかとも思うのである。このように現実にはぴったりの例はあり得ないが,仮想的なある状況をイメージすることは容易にできるという場合,これを"仮想モデル"と呼ぶことは当を得た表現といえよう。この"仮想モデル"を考察することにより,ある種の教材分野においては,その内容を理解するのに大きく役立つということがあり得る。それは確率を考えるときのサイコロの例ばかりではない。指数関数や対数関数においては,積極的に"仮想モデル"を考察することによって概念把握を深めてゆくことができるのではないかと思われる。先程例にあげたドラえもんの"バイバイン"は離散変数における指数関数の特徴を見事に捉えている。指数関数については或る段階から離散変数による指数関数から,連続変数による指数関数へと認識を深化させてゆかなければならないが,この為の"仮想モデル"はどんなものが適切なのであろうか。従来説明に用いられてきた例としては,バクテリアの分裂とか放射性元素の質量に関するものなどが多かったのではないかと思う。しかし,これらの例は私自身の体験では,高校時代から意識の底に潜む疑問の解決にはあまり役には立たなかったのである。
バクテリアの例では分裂して個数が増えてゆくというイメージがあまりにも強すぎて離散変数の変化としか受けとめられないのである。放射性元素にしても,飛び出してゆく原子には固有の質量があり,それが何個かずつ飛び出してゆくのだから元素の質量変化は,しょせん離散的な変化のはずである,とこのような意識が抜け切らないのである。これらを大量現象として観察するとき連続量化して捉えることができると説明されても,一度意識の底にしみ着いた離散的なイメージは容易に消えるものではなかったのである。連続複利法という概念なら連続変数の指数関数のモデルになり得るという話も聞いたが,今度はお金というものは一定期間を経ていないと利息がつかないという社会体験が災いして連続複利法という概念すら受けつけないのである。あげくのはてには,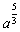 とか
とか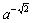 等という数は仮空のものであり,本来存在するはずもないのだ等と思い迷ったこともあった。かつて私が抱いていたこのような疑問は現在の高校生の意識の底にも潜んでいるのではなかろうか。以上のようなことを反省しつつ,連続変数による指数関数の"仮想モデル"として媒質の中を流れてゆく光に着目することにしたのである。
等という数は仮空のものであり,本来存在するはずもないのだ等と思い迷ったこともあった。かつて私が抱いていたこのような疑問は現在の高校生の意識の底にも潜んでいるのではなかろうか。以上のようなことを反省しつつ,連続変数による指数関数の"仮想モデル"として媒質の中を流れてゆく光に着目することにしたのである。
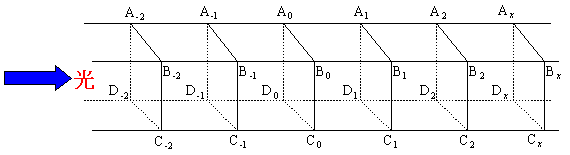
図のように直方体でできている媒質があり,光がこの中を通りぬけてゆくとする。図に書いてある直方体の中の面(例えばAxBxCxDx)を通る光の量は常に一定になるように光が流れている。光はこの内部を流れてゆきながらこの媒質に少しずつ吸収されてA0B0C0D0面を通る光の量は次第に減少し,A1B1C1D1面を通るときは光の量はa倍になっている。今媒質内を1m進むごとにa倍になるとしよう。ここからa0=1とかax+y=ax×ay,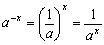 等,指数法則のすべてを導き出すことができる。しかも,x,yははじめから実数であることが確認されている。
等,指数法則のすべてを導き出すことができる。しかも,x,yははじめから実数であることが確認されている。
指数関数の学習が進んだ段階で,今度は対数関数の学習へと進む。これについては,白樺学園高校の氏家先生が工夫された"仮想モデル"がある。対数を「指数現象を見るための便利なメガネ」として導入するというものである。
"授業には厚紙を虫メガネの形に切り抜き柄の部分にlog2,log3,log10と書いたものを用意し,「この不思議なメガネで見ると・・・」等ととぼけながら進める。生徒は「全然見えない」「見えるわけないべや」などと言いながらも「何の何乗になっているか」を考えればよいことに気がつく"と氏家先生は述べておられる。(別冊資料参照)