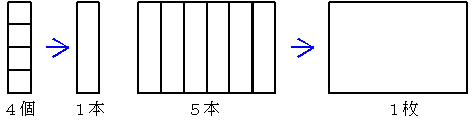
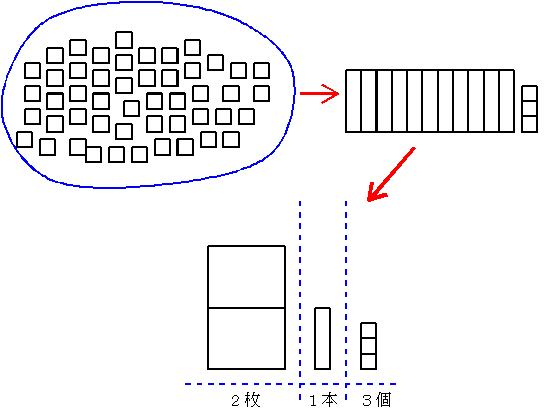
2枚と1本と3個であるが、それぞれの位でまとめ方がちがうので、これはあくまで2枚と1本と3個としかいえない。このような位取りが不等進な数え方は、時間のはかり方とか、日本の尺貫法、英国のヤード、ポンド法等にみられる。図の47個が11本と3個にまとめられ、更に2枚と1本と3個と表されるのは次のような考えから求められる。

　4個で1本とするまとめ方により11本と3個になったのは47を4で割り余りが3つで商が11だからである。引き続いて5本で1枚とするまとめ方により11本を2枚と1本とまとめ直すが、これは11を5で割ると余りが1で商が2ということを示している。

　　　47＝4×11＋3＝4(5×2＋1)＋3
　　　　＝2×4×5＋1×4＋3

　この場合の2,1,3は次のようにして求められる。

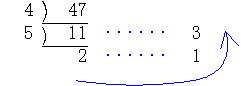
（例３）482595秒は何日、何時間、何分、何秒になるか。

（解）5日14時間3分15秒である。

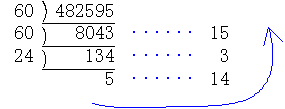
　次に異なる数で桁が上がってゆく場合について一般化してみよう。

　Ｋ₁、Ｋ₂、Ｋ₃、・・・、Ｋ_nをもとにして桁が上がってゆくものとする。まずＮをＫ₁で割り、商がq₁、余りがr₀とする。

　　Ｎ＝q₁Ｋ₁＋r₀　　(0≦r₀＜Ｋ₁)

　次に商のq₁をＫ₂で割り、商q₂、余りr₁とする。

　　q₁＝q₂Ｋ₂＋r₁　　(0≦r₁＜Ｋ₂)
　　・・・
　　q_n-1＝q_nＫ_n＋r_n-1　　(0≦r_n-1＜Ｋ_n　かつ　0＜q＜q_n＜Ｋ_n)

　故に　Ｎ＝q_nＫ₁Ｋ₂・・・Ｋ_n＋r_n-1Ｋ₁Ｋ₂・・・Ｋ_n＋・・・＋r₁Ｋ₁＋r₀