 K進法での四則演算
K進法での四則演算
3進法を例にして、加法や減法の算出の仕方について考えてみよう。
210(3)+212(3),1021(3)−112(3)
この問題を図に書くと次のようになる。
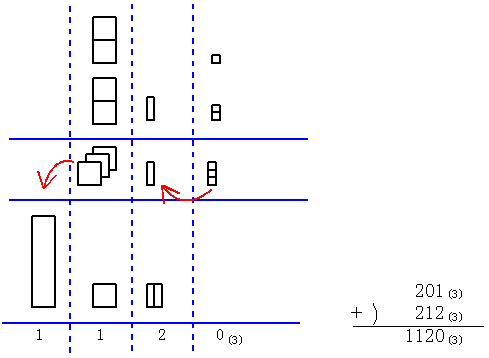
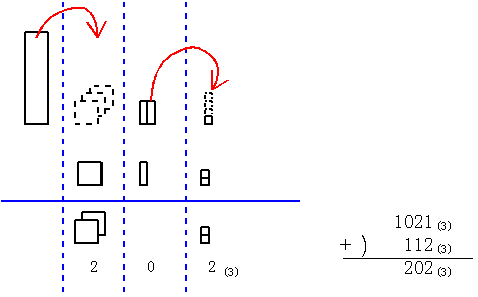
まず加法の210(3)+212(3)を図の上で考察してみよう。上の段と下の段の正方形、長方形を合併すると4枚と1本と3個であるが、3進法では3個は1本であり、3枚は大きな1本となるから結局は大1本と1枚と2本となる。このようにして3進法では3毎にくり上がるものとして計算し、くり下がりが必要なときは下の位に3がくり下げられる。
次は5進法を例として、乗法、除法について考えてみよう。
23(5)×14(5)を図の上で考察する。
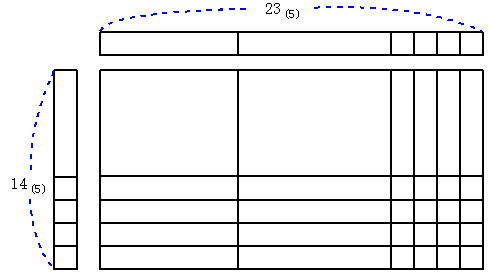
積は2枚と11本と12個となるが、5進法であるから12個は2本と2個となり、この2本と11本をあわせて13本となる。そして13本は2枚と3本になるので、全部で4枚と3本と2個になる。各部分について考えてみると12個は4個と3個の積を表し、横に並んだ8本の長方形は4個と12本の積を表し、次に縦に並んだ3本の長方形は1本と3個の積によるものであり、2枚の大正方形は1本と2本の積によるものである。そしてこれらの和が全体として4枚と3本と2個になっていて、432(5)を表している。このことから5進法の乗法についても普通の10進法における掛け算と同じように計算することができる。
ただ一つだけちがうのは10進法の掛け算が、”九九”をもとにしているのに対し、5進法の乗積表をもとにして計算してゆこうということである。
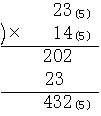
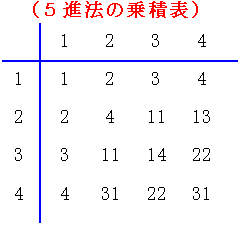
次は除法についてであるが、例えば443(5)÷14(5)についても上の乗積表を利用しつつ、次のように計算する。
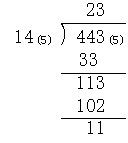
|
(例4)(1) 2進法で1011+1001,11100−1111を計算せよ。(和歌山医科大) (2) 9進法で表された7桁の数1234568に8を掛けた数を9進法で表せ。(京都薬大) |
(解)(1) 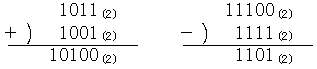
(2)
1234568(9)×8=8(1×96+2×95+3×94+4×93+5×92+6×9+8)
=+8×96+16×95+24×94+32×93
+40×92+48×9++64
=97+96+95+94+93
+92+9+1
=11111111(9)
あるいは9進法の乗積表を作り計算する。
| (例5)各桁が1或いは0から成る最高105の自然数の集合Aがある。Aの要素の個数を求めよ。また、Aが3項以上の等差列を含まないことを示せ。 |
(解)A={1,10,11,100,101,・・・,11111,100000}
これを2進数と見なして10進数に直すと、Aの要素は{1,2,3,4,・・・,32}(∵100000(2)=32)と1対1対応する。
よってAの要素は32個、Aから異なる3数x,y,zをとり、これが等差数列をなすとすると、
x+z=2y,x+yの各桁は0か1か2(今、繰り上がりをしないままで考える)、2yの各桁は0か2である。
従ってxとyのどの桁も一致して0か1でなければならない。
よって、x=zとなり矛盾する。
| (例6)105以下の自然数からうまく1983個の数を取り出すと、その中には等差列を含まないようにできることを証明せよ。(1983年数学オリンピック) |
(解)1983年の数学オリンピックの問題の中に面白い解答が紹介されていたのでその方法を示してみよう。
3進法で11111111111(11桁)を10進法に直すと
1+31+32+・・・++310=(311-1)/2=88573<105
そこで3進法で表すと各桁が0或いは1からなる最高11桁の数の集合Aを考える。
(例5)で示した如く、この集合は等差列を含まない。
Aは3進数の集合で{1,10,11,100,101,・・・,11111111111}であるが、今度はこれを2進数と考えてそれぞれ10進法に直すと順に1,2,3,・・・となり、最大の11111111111は2n-1=2047となり、Aの要素はこの集合{1,2,3,・・・2047}と1対1に対応する。するとAの要素はその中に等差列を含まず、要素を個数は2047個で1983個よりも多い。